网址:http://m.1010jiajiao.com/timu3_id_1385364[举报]
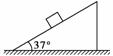
如图所示,一辆质量为M=6 kg的小车静止在光滑的水平面上,另一质量为m=2 kg的物块(可视为质点)静止在小车上的A点;在物块和小车右侧的挡板之间夹有一被压缩的轻质弹簧(弹簧和物块不相连),弹簧的弹性势能为4 J,物块和挡板之间用细线连结.已知物块和小车之间的动摩擦因数m =0.2.某时刻将细线烧断,弹簧将物块弹开,最后物块停在小车上的B点,取g=10 m/s2.

(1)分析并判定小车和物块最后对地的运动状态;
(2)A、B两点之间的距离为多少?
(3)整个过程中,小车和物块对地的位移大小分别是多少?
 如右图所示,一平面框架与水平面成37°角,宽L=0.4 m,上、下两端各有一个电阻R0=1 Ω,框架的其他部分电阻不计,框架足够长.垂直于框平面的方向存在向上的匀强磁场,磁感应强度B=2T.ab为金属杆,其长度为L=0.4 m,质量m=0.8 kg,电阻r=0.5Ω,棒与框架的动摩擦因数μ=0.5.由静止开始下滑,直到速度达到最大的过程中,上端电阻R0产生的热量Q0=0.375J(已知sin37°=0.6,cos37°=0.8;g取10m/s2)求:
如右图所示,一平面框架与水平面成37°角,宽L=0.4 m,上、下两端各有一个电阻R0=1 Ω,框架的其他部分电阻不计,框架足够长.垂直于框平面的方向存在向上的匀强磁场,磁感应强度B=2T.ab为金属杆,其长度为L=0.4 m,质量m=0.8 kg,电阻r=0.5Ω,棒与框架的动摩擦因数μ=0.5.由静止开始下滑,直到速度达到最大的过程中,上端电阻R0产生的热量Q0=0.375J(已知sin37°=0.6,cos37°=0.8;g取10m/s2)求:
(1)杆ab的最大速度;
(2)从开始到速度最大的过程中ab杆沿斜面下滑的距离;在该过程中通过ab的电荷量.
查看习题详情和答案>>
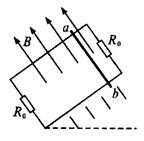 如右图所示,一平面框架与水平面成37°角,宽L=0.4 m,上、下两端各有一个电阻R0=1 Ω,框架的其他部分电阻不计,框架足够长.垂直于框平面的方向存在向上的匀强磁场,磁感应强度B=2T.ab为金属杆,其长度为L=0.4 m,质量m=0.8 kg,电阻r=0.5Ω,棒与框架的动摩擦因数μ=0.5.由静止开始下滑,直到速度达到最大的过程中,上端电阻R0产生的热量Q0=0.375J(已知sin37°=0.6,cos37°=0.8;g取10m/s2)求:
如右图所示,一平面框架与水平面成37°角,宽L=0.4 m,上、下两端各有一个电阻R0=1 Ω,框架的其他部分电阻不计,框架足够长.垂直于框平面的方向存在向上的匀强磁场,磁感应强度B=2T.ab为金属杆,其长度为L=0.4 m,质量m=0.8 kg,电阻r=0.5Ω,棒与框架的动摩擦因数μ=0.5.由静止开始下滑,直到速度达到最大的过程中,上端电阻R0产生的热量Q0=0.375J(已知sin37°=0.6,cos37°=0.8;g取10m/s2)求:
(1)杆ab的最大速度;
(2)从开始到速度最大的过程中ab杆沿斜面下滑的距离;在该过程中通过ab的电荷量.
查看习题详情和答案>>