0 137362 137370 137376 137380 137386 137388 137392 137398 137400 137406 137412 137416 137418 137422 137428 137430 137436 137440 137442 137446 137448 137452 137454 137456 137457 137458 137460 137461 137462 137464 137466 137470 137472 137476 137478 137482 137488 137490 137496 137500 137502 137506 137512 137518 137520 137526 137530 137532 137538 137542 137548 137556 447348
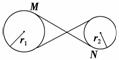
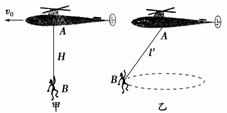
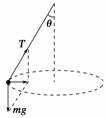

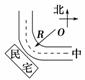

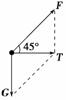 根据题意有G=mg=350 N;则由图易得女运动员受到的拉力约为350 N,A正确;向心加速度约为10 m/s2,C正确.
根据题意有G=mg=350 N;则由图易得女运动员受到的拉力约为350 N,A正确;向心加速度约为10 m/s2,C正确.