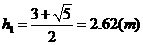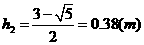0 137279 137287 137293 137297 137303 137305 137309 137315 137317 137323 137329 137333 137335 137339 137345 137347 137353 137357 137359 137363 137365 137369 137371 137373 137374 137375 137377 137378 137379 137381 137383 137387 137389 137393 137395 137399 137405 137407 137413 137417 137419 137423 137429 137435 137437 137443 137447 137449 137455 137459 137465 137473 447348
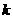 倍.中子与原子核的每次碰撞都可看成是弹性正碰.设每次碰撞前原子核可认为是静止的,求
倍.中子与原子核的每次碰撞都可看成是弹性正碰.设每次碰撞前原子核可认为是静止的,求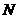 次碰撞后中子速率与原速率之比.
次碰撞后中子速率与原速率之比.
 和
和 ,碰撞后速度分别为
,碰撞后速度分别为 和
和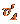 ,碰撞前后的总动量和总能量守恒,有
,碰撞前后的总动量和总能量守恒,有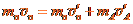 ①
①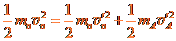 ②
②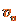 为碰撞前中子速度,由题设
为碰撞前中子速度,由题设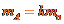 ③
③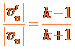 ④
④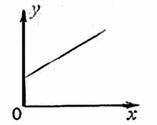
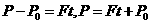 说明动量和时间是线性关系,纵截距为初动量,C正确。结合
说明动量和时间是线性关系,纵截距为初动量,C正确。结合 得
得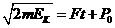 ,说明动能和时间的图像是抛物线,A错误。根据光电效应方程
,说明动能和时间的图像是抛物线,A错误。根据光电效应方程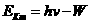 ,说明最大初动能和时间是线性关系,但纵截距为负值,B错误。当磁感应强度随时间均匀增大时,增长合回路内的磁通量均匀增大,根据法拉第电磁感应定律增长合回路的感应电动势等于磁通量的变化率,是一个定值,不随时间变化,D错误。
,说明最大初动能和时间是线性关系,但纵截距为负值,B错误。当磁感应强度随时间均匀增大时,增长合回路内的磁通量均匀增大,根据法拉第电磁感应定律增长合回路的感应电动势等于磁通量的变化率,是一个定值,不随时间变化,D错误。 .使木板与重物以共同的速度
.使木板与重物以共同的速度 向右运动,某时刻木板与墙发生弹性碰撞,碰撞时间极短.求木板从第一次与墙碰撞到再次碰撞所经历的时间.设木板足够长,重物始终在木板上.重力加速度为g.
向右运动,某时刻木板与墙发生弹性碰撞,碰撞时间极短.求木板从第一次与墙碰撞到再次碰撞所经历的时间.设木板足够长,重物始终在木板上.重力加速度为g.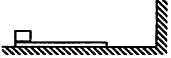
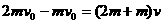 ,解得:
,解得: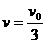
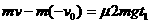
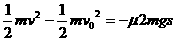

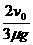 +
+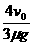
 。
。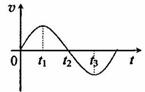
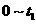 时间内,外力做正功
时间内,外力做正功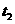 时刻,外力的功率最大
时刻,外力的功率最大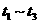 时间内,外力做的总功为零
时间内,外力做的总功为零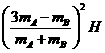

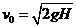 ①
①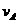 和
和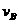 ,以竖直向上为速度的正方向,根据A、B组成的系统动量守恒和动能守恒得
,以竖直向上为速度的正方向,根据A、B组成的系统动量守恒和动能守恒得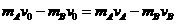 ②
② 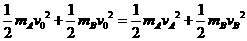 ③
③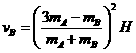 ④
④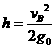 ⑤
⑤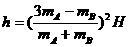 ⑥
⑥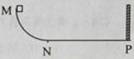
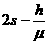 或
或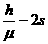
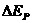 与物块克服摩擦力所做功的数值相等。
与物块克服摩擦力所做功的数值相等。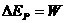 ①
①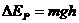 ②
②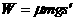 ③
③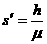 ④
④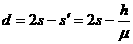 ⑤
⑤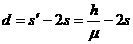 ⑥
⑥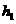 和
和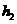 的圆轨道上运动时,周期分别为
的圆轨道上运动时,周期分别为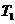 和
和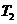 。火星可视为质量分布均匀的球体,且忽略火星的自转影响,万有引力常量为G。仅利用以上数据,可以计算出
。火星可视为质量分布均匀的球体,且忽略火星的自转影响,万有引力常量为G。仅利用以上数据,可以计算出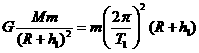 ;
;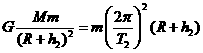 ,可求得火星的质量
,可求得火星的质量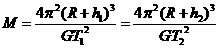 和火星的半径
和火星的半径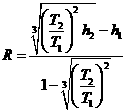 ,根据密度公式得:
,根据密度公式得: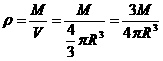 。在火星表面的物体有
。在火星表面的物体有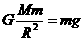 ,可得火星表面的重力加速度
,可得火星表面的重力加速度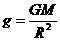 ,故选项A正确。
,故选项A正确。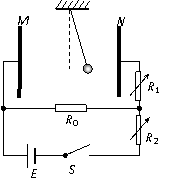 (安徽卷)24.(20分)如图,ABD为竖直平面内的光滑绝缘轨道,其中AB段是水平的,BD段为半径R=0.2m的半圆,两段轨道相切于B点,整个轨道处在竖直向下的匀强电场中,场强大小E=5.0×103V/m。一不带电的绝缘小球甲,以速度υ0沿水平轨道向右运动,与静止在B点带正电的小球乙发生弹性碰撞。已知甲、乙两球的质量均为m=1.0×10-2kg,乙所带电荷量q=2.0×10-5C,g取10m/s2。(水平轨道足够长,甲、乙两球可视为质点,整个运动过程无电荷转移)
(安徽卷)24.(20分)如图,ABD为竖直平面内的光滑绝缘轨道,其中AB段是水平的,BD段为半径R=0.2m的半圆,两段轨道相切于B点,整个轨道处在竖直向下的匀强电场中,场强大小E=5.0×103V/m。一不带电的绝缘小球甲,以速度υ0沿水平轨道向右运动,与静止在B点带正电的小球乙发生弹性碰撞。已知甲、乙两球的质量均为m=1.0×10-2kg,乙所带电荷量q=2.0×10-5C,g取10m/s2。(水平轨道足够长,甲、乙两球可视为质点,整个运动过程无电荷转移)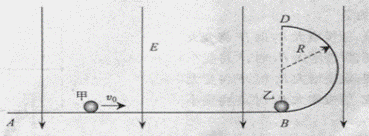
 (3)
(3) <
<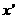 <
<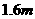
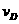 ,乙离开D点达到水平轨道的时间为t,乙的落点到B点的距离为
,乙离开D点达到水平轨道的时间为t,乙的落点到B点的距离为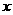 ,则
,则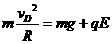 ①
①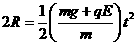 ②
②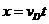 ③
③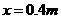 ④
④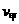 、
、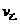 ,根据动量守恒和机械能守恒定律有:
,根据动量守恒和机械能守恒定律有: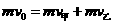 ⑤
⑤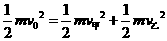 ⑥
⑥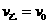 ⑦
⑦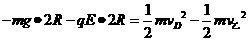 ⑧
⑧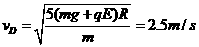 ⑨
⑨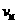 、
、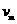 ,根据动量守恒和机械能守恒定律有:
,根据动量守恒和机械能守恒定律有: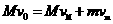 (10)
(10)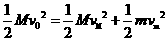 (11)
(11)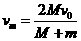 (12)
(12)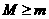 ,可得:
,可得: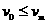 <
<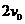 (13)
(13)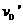 ,由动能定理得
,由动能定理得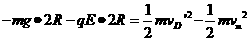 (14)
(14)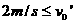 <
<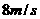 (15)
(15)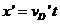 (16)
(16)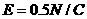 的竖直向下的匀强电场,长
的竖直向下的匀强电场,长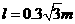 的不可伸长的轻绳一端固定于O点,另一端系一质量
的不可伸长的轻绳一端固定于O点,另一端系一质量 的不带电小球
的不带电小球 ,拉起小球至绳水平后,无初速释放。另一电荷量
,拉起小球至绳水平后,无初速释放。另一电荷量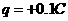 、质量与
、质量与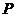 ,以速度
,以速度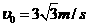 水平抛出,经时间
水平抛出,经时间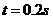 与小球
与小球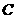 与
与 点下方一足够大的平板相遇。不计空气阻力,小球均可视为质点,取
点下方一足够大的平板相遇。不计空气阻力,小球均可视为质点,取 。
。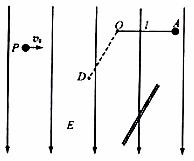
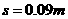 到达平板,此时速度恰好为0,求所加的恒力。
到达平板,此时速度恰好为0,求所加的恒力。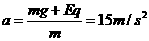
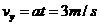
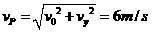
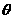 ,由于P与A迎面正碰,则P与A速度方向相反,所以P的速度与水平方向的夹角为
,由于P与A迎面正碰,则P与A速度方向相反,所以P的速度与水平方向的夹角为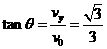 ,
,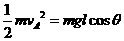
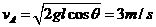
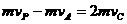
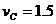 m/s
m/s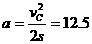 m/s2
m/s2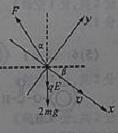
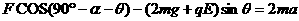
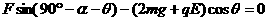
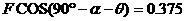
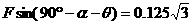
 α=30°
α=30°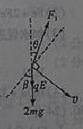
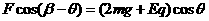
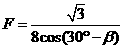 (其中0≤β<120°)
(其中0≤β<120°)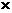
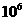 m的卫星,c是地球同步卫星,某一时刻b、c刚好位于a的正上方(如图甲所示),经48h,a、b、c的大致位置是图乙中的(取地球半径R=6.4
m的卫星,c是地球同步卫星,某一时刻b、c刚好位于a的正上方(如图甲所示),经48h,a、b、c的大致位置是图乙中的(取地球半径R=6.4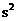 ,
, =
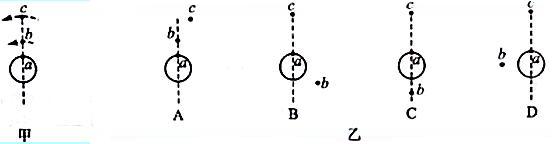
=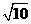 )
)
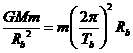 ,GM=R2,化简得
,GM=R2,化简得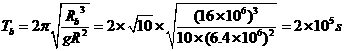
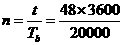 =8.64,所以B正确。
=8.64,所以B正确。 的道向下运动到B点后水平滑出,最后落在水池中。设滑道的水平距离为L,B点的高度h可由运动员自由调节(取;g=10m/s2)。求:
的道向下运动到B点后水平滑出,最后落在水池中。设滑道的水平距离为L,B点的高度h可由运动员自由调节(取;g=10m/s2)。求: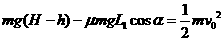 ①
①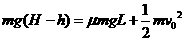 ②
②
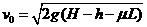 ③
③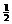 gt2
⑤
gt2
⑤
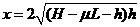 ⑥
⑥