试卷类型:A
江门市2009年高考第二次模拟考试
数 学(理科)
本试卷共4页,21小题,满分150分。考试用时120分钟。
注意事项:⒈答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。用2B铅笔将试卷类型(A)填涂在答题卡相应位置上。将条形码横贴在答题卡右上角“条形码粘贴处”。
⒉选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
⒊非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。不按以上要求作答的答案无效。
⒋作答选做题时,请先用2B铅笔填涂选做题的题号(或题组号)对应的信息点,再作答。漏涂、错涂、多涂的,答案无效。
⒌考生必须保持答题卡的整洁。考试结束后,将试卷和答题卡一并交回。
参考公式:锥体的体积公式 ,其中
,其中 是锥体的底面积,
是锥体的底面积, 是锥体的高.
是锥体的高.
方差的公式 ,其中是
,其中是 样本平均数.
样本平均数.
一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
⒈已知函数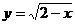 的定义域为
的定义域为 ,集合
,集合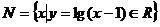 ,则
,则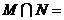
A.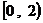 B.
B.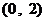 C.
C. D.
D.
⒉在复平面内,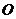 是原点,向量
是原点,向量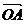 对应的复数是
对应的复数是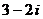 (
(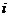 为虚数单位),
为虚数单位),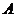 关于虚轴的对称点为
关于虚轴的对称点为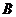 ,则向量
,则向量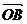 对应的复数是
对应的复数是
A.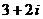 B.
B.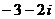 C.
C.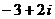 D.
D. 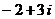
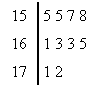 ⒊图1是根据某校10位高一同学的身高(单位:
⒊图1是根据某校10位高一同学的身高(单位: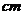 )画出的茎叶图,
)画出的茎叶图,
其中左边的数字从左到右分别表示学生身高的百位数字和十位数字,
右边的数字表示学生身高的个位数字,从图中可以得到这10位同学
 身高的中位数是
身高的中位数是
A. 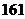
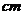 B.
B. 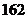
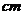 C.
C. 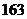
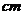 D.
D. 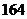
⒋双曲线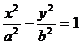 的焦距为4,一个顶点是抛物线
的焦距为4,一个顶点是抛物线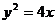 的焦点,则双曲线的离心率
的焦点,则双曲线的离心率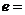
A.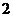 B.
B.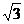 C.
C.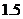 D.
D.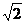
⒌已知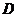 是
是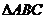 所在平面内一点,
所在平面内一点,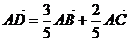 .则
.则
A.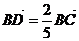 B.
B.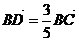 C.
C.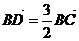 D.
D.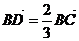
⒍已知平面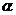 、
、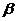 和不在这两个平面内的两直线
和不在这两个平面内的两直线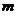 、
、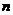 ,下列命题中
,下列命题中
命题1:若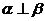 ,
,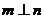 ,
,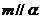 ,则
,则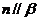
命题2:若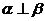 ,
,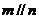 ,
,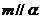 ,则
,则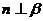
命题3:若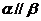 ,
,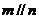 ,
,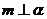 ,则
,则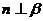
命题4:若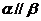 ,
,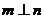 ,
,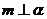 ,则
,则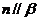
真命题的个数是
A.  个 B.
个 B. 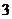 个 C.
个 C. 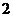 个 D.
个 D. 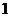 个
个
⒎已知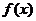 是定义在实数集
是定义在实数集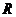 上的奇函数,对
上的奇函数,对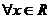 ,
,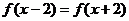 ,当
,当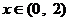 时,
时, ,则
,则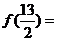
A. B.
B.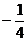 C.
C.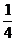 D.
D. 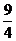
⒏平面直角坐标系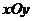 中,曲线
中,曲线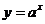 (
(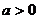 且
且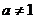 )在第二象限的部分都在不等式
)在第二象限的部分都在不等式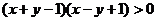 表示的平面区域内,则
表示的平面区域内,则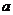 的取值范围是
的取值范围是
A.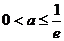 B.
B.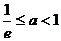 C.
C.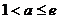 D.
D.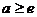
㈠必做题(9~12题)
二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分.
⒐已知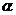 是第二象限角,
是第二象限角,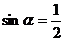 ,则
,则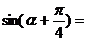 .
.
⒑平面直角坐标系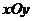 中,已知点
中,已知点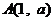 (
(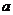 是常数)、
是常数)、 ,直线
,直线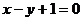 与线段
与线段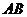 相交,则
相交,则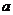 的取值范围是
.
的取值范围是
.
⒒空间直角坐标系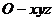 有8个点:
有8个点: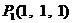 、
、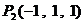 、…、
、…、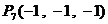 、
、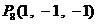 (每个点的横、纵、竖坐标都是
(每个点的横、纵、竖坐标都是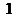 或
或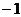 ),以其中4个点为顶点的三棱锥一共有
个(用数字作答).
),以其中4个点为顶点的三棱锥一共有
个(用数字作答).
⒓一个数列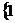 ,2,2,3,3,3,4,4,4,4,5,
,2,2,3,3,3,4,4,4,4,5,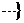 ,它的首项是
,它的首项是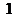 ,随后两项都是
,随后两项都是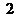 ,接下来3项都是
,接下来3项都是 ,再接下来4项都是
,再接下来4项都是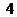 ,…,依此类推,若
,…,依此类推,若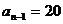 ,
,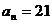 ,则
,则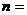 .
.
㈡选做题(13~15题,考生只能从中选做两题)
⒔(坐标系与参数方程选做题)在极坐标系中,曲线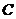 的极坐标方程为
的极坐标方程为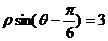 ,点
,点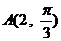 到曲线
到曲线 上点的距离的最小值
上点的距离的最小值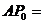 .
.
 ⒕(不等式选讲选做题)已知
⒕(不等式选讲选做题)已知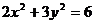 ,则
,则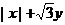 的最大值
的最大值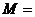 .
.
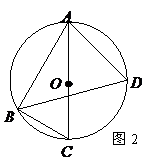
⒖(几何证明选讲选选做题)如图2, 是⊙
是⊙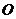 的直径,
的直径,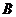 是
是
⊙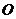 上一点,
上一点,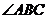 的平分线与⊙
的平分线与⊙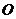 相交于
相交于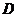 .已知
.已知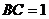 ,
,
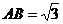 ,则
,则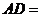 ;过
;过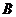 、
、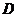 分别作⊙
分别作⊙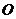 的切线,则
的切线,则
这两条切线的夹角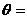 .
.
三、解答题:本大题共6小题,满分80分。解答须写出文字说明、证明过程和演算步骤.
⒗(本小题满分13分)设函数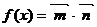 ,其中
,其中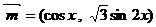 ,
,
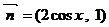 .
.
⑴求函数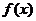 的单调增区间;
的单调增区间;
⑵在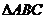 中,
中,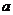 、
、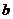 、
、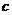 分别是角
分别是角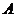 、
、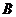 、
、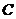 的对边,
的对边,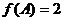 ,
,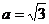 ,
,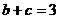 ,求
,求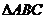 的面积.
的面积.
⒘(本小题满分13分)某批发市场对某种商品的日销售量(单位:吨)进行统计,最近50天的统计结果如下:
日销售量
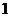
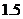
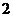
频数
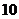
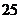
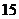
频率
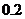
⑴填充上表;
⑵若以上表频率作为概率,且每天的销售量相互独立.
①5天中该种商品恰好有2天的销售量为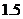 吨的概率;
吨的概率;
②已知每吨该商品的销售利润为2千元,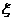 表示该种商品两天销售利润的和(单位:千元),求
表示该种商品两天销售利润的和(单位:千元),求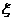 的分布列和数学期望.
的分布列和数学期望.
⒙(本小题满分14分)在平面直角坐标系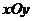 中,直线
中,直线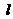 :
: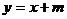 与椭圆
与椭圆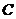 :
: 相交于
相交于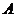 、
、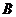 两点,且
两点,且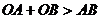 .
.
⑴求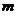 的取值范围;
的取值范围;
⑵若以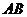 为直径的圆经过
为直径的圆经过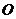 点,求直线
点,求直线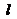 的方程.
的方程.
 ⒚(本小题满分14分)如图3,直四棱柱
⒚(本小题满分14分)如图3,直四棱柱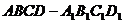 的底面
的底面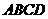 是菱形,
是菱形,
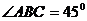 ,其侧面展开图是边长为
,其侧面展开图是边长为 的正方形。
的正方形。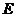 、
、
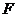 分别是侧棱
分别是侧棱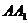 、
、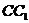 上的动点,
上的动点,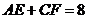 .
.
⑴证明: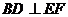 ;
;
⑵当 时,求面
时,求面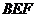 与底面
与底面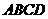
所成二面角的正弦值;
⑶多面体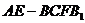 的体积
的体积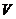 是否为常数?
是否为常数?
若是,求这个常数,若不是,求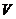 的取值范围.
的取值范围.
⒛(本小题满分13分)已知函数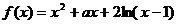 ,
,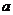 是常数.
是常数.
⑴证明曲线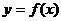 在点
在点 的切线经过
的切线经过 轴上一个定点;
轴上一个定点;
⑵若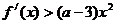 对
对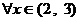 恒成立,求
恒成立,求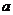 的取值范围;
的取值范围;
(参考公式: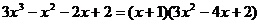 )
)
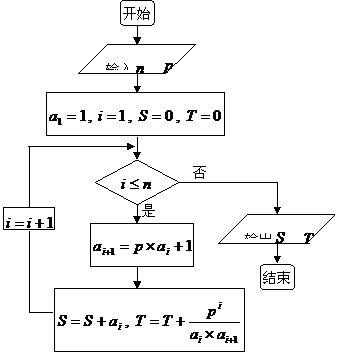 ⑶讨论函数
⑶讨论函数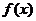 的单调区间.
的单调区间.
21.(本小题满分13分)下面的程序框图给出数列
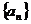 (
(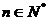 ,下同)的递推关系,计算并输出
,下同)的递推关系,计算并输出
数列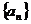 和
和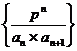 前若干项之和
前若干项之和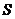 、
、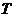 .
.
⑴若输入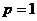 ,
,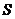 满足
满足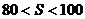 ,求
,求
输入的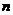 的值;
的值;
⑵若输入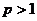 ,
,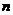 ,求输出的
,求输出的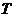 的值.
的值.
(用关于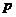 、
、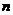 的代数式表示)
的代数式表示)
理科数学评分参考
二、填空题 ⒐  ⒑
⒑ ⒒
⒒ ⒓
⒓ 
⒔ 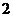 ⒕
⒕ 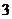 ⒖
⒖ 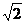 ……3分 ;
……3分 ;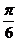 (或
(或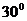 )
)
三、解答题
⒗⑴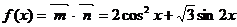 ……2分,
……2分,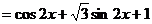 ……3分,
……3分,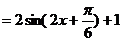 ……4分,当
……4分,当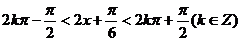 即
即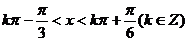 时,
时,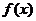 单调增加……5分,所以
单调增加……5分,所以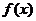 的单调增区间是
的单调增区间是 ……6分(包含或不包含区间端点均可,但要前后一致).
……6分(包含或不包含区间端点均可,但要前后一致).
⑵解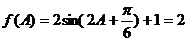 ,
,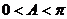 …7分,得
…7分,得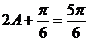 ,
,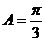 …9分,由余弦定理
…9分,由余弦定理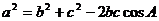 得
得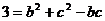 …10分,解
…10分,解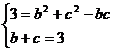 …11分,得
…11分,得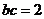 …12分,所以
…12分,所以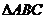 的面积为
的面积为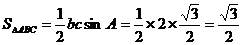 …13分.
…13分.
⒘⑴从左至右两空格依次是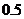 、
、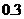 ……2分
……2分
⑵①依题意,随机选取一天,销售量为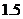 吨的概率
吨的概率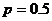 ……3分
……3分
设5天中该种商品有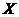 天的销售量为
天的销售量为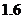 吨,则
吨,则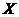 ~
~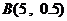 ……4分
……4分
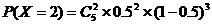 ……6分,
……6分,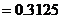 ……7分
……7分
②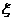 的可能取值为4,5,6,7,8……8分
的可能取值为4,5,6,7,8……8分
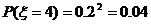 ,
,
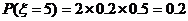

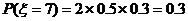
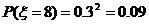 ……10分(对2、3、4个给1分,全对给2分)
……10分(对2、3、4个给1分,全对给2分)
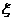
4
5
6
7
8
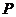
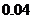
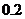
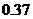
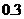

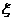 的分布列为
的分布列为
……11分
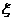 的数学期望为
的数学期望为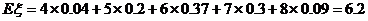 (千元)
(千元)
……13分(列式1分,计算1分).
⒙⑴解方程组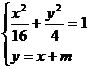 ……1分,得
……1分,得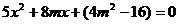 ……2分
……2分
因为直线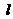 椭圆
椭圆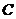 有两个交点,所以
有两个交点,所以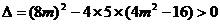 ……4分,解得
……4分,解得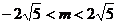 ……5分,又因为
……5分,又因为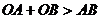 ,所以
,所以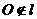 ,
,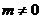 ,所以
,所以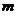 的取值范围是
的取值范围是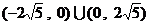 ……6分.
……6分.
⑵设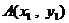 、
、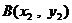 ,由⑴得
,由⑴得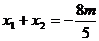 ,
,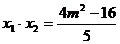 ……7分,
……7分,
以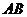 为直径的圆经过
为直径的圆经过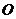 点,所以
点,所以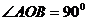 ……8分,
……8分,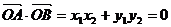 ……9分,由
……9分,由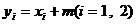 ……10分,得
……10分,得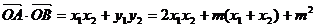
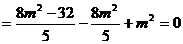 ……12分,解得
……12分,解得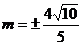 ……13分,所以直线
……13分,所以直线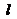 的方程是
的方程是
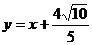 或
或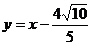 ……14分.
……14分.
⒚⑴连接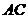 ,因为
,因为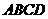 是菱形,所以
是菱形,所以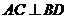 ……1分,因为
……1分,因为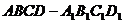 是直四棱柱,
是直四棱柱,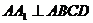 ,
,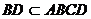 ,所以
,所以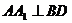 ……2分,因为
……2分,因为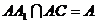 ,所以
,所以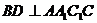 ……3分,因为
……3分,因为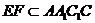 ,所以
,所以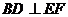 ……4分.
……4分.
⑵设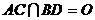 ,以
,以 为原点,
为原点,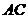 、
、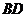 分别为
分别为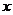 轴、
轴、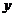 轴建立空间直角坐标系
轴建立空间直角坐标系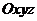
……5分,依题意,菱形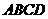 的边长为
的边长为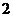 ,棱柱侧棱长为
,棱柱侧棱长为 ,所以
,所以 ,
,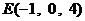 、
、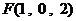 ……6分,设平面
……6分,设平面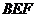 的一个法向量为
的一个法向量为 ,则
,则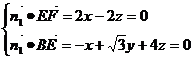 ……7分,解得
……7分,解得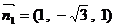 ……8分,底面
……8分,底面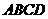 的一个法向量为
的一个法向量为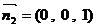 ,设面
,设面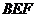 与底面
与底面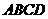 所成二面角的大小为
所成二面角的大小为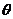 ,则
,则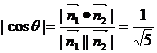 ,
,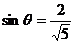 ……9分.
……9分.
⑶多面体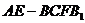 是四棱锥
是四棱锥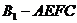 和三棱锥
和三棱锥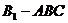 的组合体……10分,依题意,
的组合体……10分,依题意,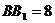 ,
,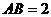 ……11分,
……11分,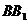 三棱锥
三棱锥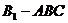 的高,
的高,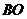 是四棱锥
是四棱锥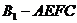 的高…12分,所以
的高…12分,所以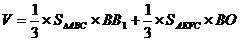 …13分,
…13分,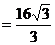 是常数…14分.
是常数…14分.
⒛⑴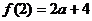 ,
, ,
,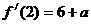 ……1分,曲线
……1分,曲线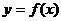 在点
在点 的切线为
的切线为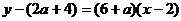 ……2分,当
……2分,当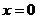 时,由切线方程得
时,由切线方程得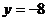 ,所以切线经过
,所以切线经过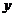 轴上的定点
轴上的定点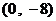 ……3分.
……3分.
⑵由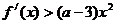 得
得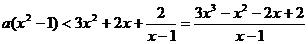 ……4分,对
……4分,对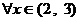 ,
,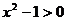 ,所以
,所以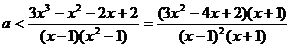
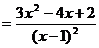 ……5分,设
……5分,设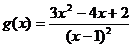 ,则
,则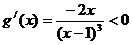 ……6分,
……6分,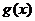 在区间
在区间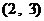 单调递减……7分,所以
单调递减……7分,所以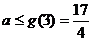 ,
,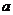 的取值范围为
的取值范围为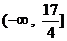 ……8分.
……8分.
⑶函数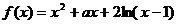 的定义域为
的定义域为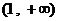 ,
,
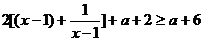 ……9分.
……9分.
若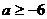 ,则
,则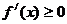 ,
,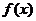 在定义域
在定义域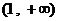 上单调增加……10分;
上单调增加……10分;
若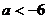 ,解方程
,解方程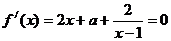 得
得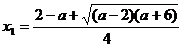 ,
,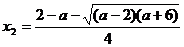 ……11分,
……11分,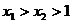 ,当
,当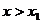 或
或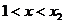 时,
时,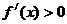 ;
;
当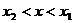 时,
时,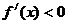 ……12分,所以
……12分,所以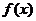 的单调增区间是
的单调增区间是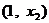 和
和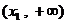 ,单调减区间是
,单调减区间是 (区间无论包含端点
(区间无论包含端点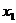 、
、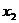 均可,但要前后一致)……13分.
均可,但要前后一致)……13分.
21.⑴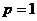 ,
,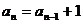 ,
,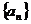 (
(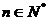 )是首项为
)是首项为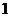 、公差为
、公差为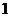 的等差数列……1分,所以
的等差数列……1分,所以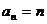 ……2分,
……2分,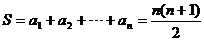 ……3分,解
……3分,解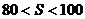 即
即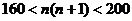 ,
,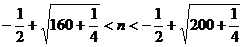 ,
,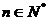 ,
,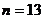 ……5分.
……5分.
⑵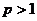 ,
,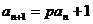 ,
,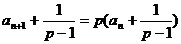 ……7分,
……7分,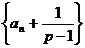 (
(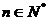 )是首项为
)是首项为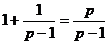 、公比为
、公比为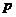 的等比数列……8分,所以
的等比数列……8分,所以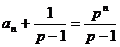 ,
,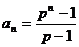 ……9分,
……9分,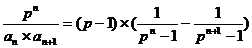 ……11分,所以
……11分,所以
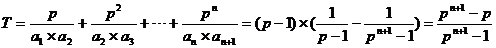 ……13分.
……13分.