摘要:⒑平面直角坐标系中.已知点(是常数)..直线与线段相交.则的取值范围是 .
网址:http://m.1010jiajiao.com/timu_id_316146[举报]
在平面直角坐标系中,已知向量
=(c,0)(c为常数,且c>0),
=(x,x)(x∈R),|
|的最小值为1,
=(
,t)(a为常数,且a>c,t∈R).动点P同时满足下列三个条件:
(1)|
|=
|
|;(2)
=λ•
(λ∈R,且λ≠0);
(2)动点P的轨迹C经过点B(0,-1).
(Ⅰ)求曲线C的方程;
(Ⅱ)是否存在方向向量为m=(1,k)(k≠0)的直线l,l与曲线C相交于M、N两点,使|
|=|
|,且
与
的夹角为60°?若存在,求出k值,并写出直线l的方程;若不存在,请说明理由.
查看习题详情和答案>>
| OF |
| OG |
| FG |
| OE |
| a2 |
| C |
(1)|
| PF |
| c |
| a |
| PE |
| PE |
| OF |
(2)动点P的轨迹C经过点B(0,-1).
(Ⅰ)求曲线C的方程;
(Ⅱ)是否存在方向向量为m=(1,k)(k≠0)的直线l,l与曲线C相交于M、N两点,使|
| BM |
| BN |
| BM |
| BN |
在平面直角坐标系中,已知A(-1,2),B(0,x2+2),C(x+2tanθ-1,y+3)三点共线.θ为常数且θ∈(-
,
).
(1)求y关于x的函数y=f (x)的表达式;
(2)是否存在常数tanθ,使函数y=f (x)在[-1,
]上的最小值为tanθ?如果存在,求出tanθ,如果不存在,说明理由.
查看习题详情和答案>>
| π |
| 2 |
| π |
| 2 |
(1)求y关于x的函数y=f (x)的表达式;
(2)是否存在常数tanθ,使函数y=f (x)在[-1,
| 3 |
在平面直角坐标系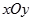 中,已知圆
中,已知圆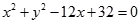 的圆心为
的圆心为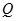 ,过点
,过点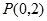 且斜率为
且斜率为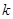 的直线与圆
的直线与圆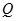 相交于不同的两点
相交于不同的两点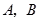 .
.
(Ⅰ)求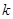 的取值范围;
的取值范围;
(Ⅱ)以OA,OB为邻边作平行四边形OADB,是否存在常数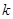 ,使得直线OD与PQ平行?如果存在,求
,使得直线OD与PQ平行?如果存在,求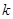 值;如果不存在,请说明理由.
值;如果不存在,请说明理由.
查看习题详情和答案>>
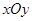 中,已知圆
中,已知圆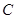 经过点
经过点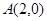 和点
和点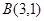 ,且圆心
,且圆心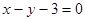 上,过点
上,过点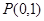 且斜率为
且斜率为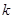 的直线与圆
的直线与圆 .
.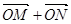 与
与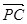 共线?如果存在,求
共线?如果存在,求 中,已知圆
中,已知圆 的圆心为
的圆心为 ,过点
,过点 且斜率为
且斜率为 的直线与圆
的直线与圆 .
.