网址:http://m.1010jiajiao.com/timu_id_316191[举报]
已知函数 .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)设 ,若对任意
,若对任意 ,
, ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
【解析】第一问利用 的定义域是
的定义域是

由x>0及 得1<x<3;由x>0及
得1<x<3;由x>0及 得0<x<1或x>3,
得0<x<1或x>3,
故函数 的单调递增区间是(1,3);单调递减区间是
的单调递增区间是(1,3);单调递减区间是
第二问中,若对任意 不等式
不等式 恒成立,问题等价于
恒成立,问题等价于 只需研究最值即可。
只需研究最值即可。
解: (I) 的定义域是
的定义域是 ......1分
......1分
 ............. 2分
............. 2分
由x>0及 得1<x<3;由x>0及
得1<x<3;由x>0及 得0<x<1或x>3,
得0<x<1或x>3,
故函数 的单调递增区间是(1,3);单调递减区间是
的单调递增区间是(1,3);单调递减区间是 ........4分
........4分
(II)若对任意 不等式
不等式 恒成立,
恒成立,
问题等价于 ,
.........5分
,
.........5分
由(I)可知,在 上,x=1是函数极小值点,这个极小值是唯一的极值点,
上,x=1是函数极小值点,这个极小值是唯一的极值点,
故也是最小值点,所以 ; ............6分
; ............6分

当b<1时, ;
;
当 时,
时, ;
;
当b>2时, ;
............8分
;
............8分
问题等价于
 ........11分
........11分
解得b<1 或 或
或  即
即 ,所以实数b的取值范围是
,所以实数b的取值范围是
查看习题详情和答案>>
已知函数 在
在 取得极值
取得极值
(1)求 的单调区间(用
的单调区间(用 表示);
表示);
(2)设 ,
, ,若存在
,若存在 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围.
【解析】第一问利用

根据题意 在
在 取得极值,
取得极值, 
对参数a分情况讨论,可知
当 即
即 时递增区间:
时递增区间:  递减区间:
递减区间:  ,
,

当 即
即 时递增区间:
时递增区间:  递减区间:
递减区间:  ,
,

第二问中, 由(1)知:
由(1)知:  在
在 ,
,

 ,
,
 在
在


从而求解。
解: 
 …..3分
…..3分
 在
在 取得极值,
取得极值,  ……………………..4分
……………………..4分
(1) 当 即
即 时 递增区间:
时 递增区间:  递减区间:
递减区间:  ,
,

当 即
即 时递增区间:
时递增区间:  递减区间:
递减区间:  ,
,
 ………….6分
………….6分
(2)  由(1)知:
由(1)知:  在
在 ,
,

 ,
,
 在
在

 ……………….10分
……………….10分
 , 使
, 使 成立
成立



 得:
得: 
查看习题详情和答案>>
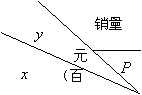
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,|AB|=3米,|AD|=2米,
(I)要使矩形AMPN的面积大于32平方米,则AN的长应在什么范围内?
(II)当AN的长度是多少时,矩形AMPN的面积最小?并求出最小面积.
(Ⅲ)若AN的长度不少于6米,则当AN的长度是多少时,矩形AMPN的面积最小?并求出最小面积.

【解析】本题主要考查函数的应用,导数及均值不等式的应用等,考查学生分析问题和解决问题的能力 第一问要利用相似比得到结论。
(I)由SAMPN > 32 得 > 32 ,
> 32 ,
∵x >2,∴ ,即(3x-8)(x-8)> 0
,即(3x-8)(x-8)> 0
∴2<X<8/3,即AN长的取值范围是(2,8/3)或(8,+ )
)
第二问, 
当且仅当
(3)令
∴当x
> 4,y′> 0,即函数y= 在(4,+∞)上单调递增,∴函数y=
在(4,+∞)上单调递增,∴函数y= 在[6,+∞]上也单调递增.
在[6,+∞]上也单调递增.
∴当x=6时y= 取得最小值,即SAMPN取得最小值27(平方米).
取得最小值,即SAMPN取得最小值27(平方米).
查看习题详情和答案>>
月饼是一种时间性很强的商品,若在中秋节前出售,每盒将获利5元,若到中秋节还没能及时售完,中秋节之后只能降价出售,每盒将亏损3元.根据市场调查,销量![]() (百盒)的概率分布如下:
(百盒)的概率分布如下:
| 销量 | 1 | 2 | 3 | 4 | 5 |
|
| 0.05 | 0.25 | 0.3 | 0.3 | 0.1 |
由于市场风险较大,批发商要求零售商预订月饼的数量,且每年只预订一次,订货量以百盒为单位.
⑴.设订购量为![]() 百盒时,获利额为
百盒时,获利额为![]() 元.下表表示与
元.下表表示与![]() 对应的
对应的![]() 的分布列,请在空格处填入适当的
的分布列,请在空格处填入适当的![]() 值,并计算相应的获利期望值
值,并计算相应的获利期望值![]() ;
;
⑵.预订多少盒月饼最合理?
|
| 1 | 2 | 3 | 4 | 5 |
|
| 0.05 | 0.25 | 0.3 | 0.3 | 0.1 | ||
| 1 | 500 | 500 | 500 | 500 | 500 | 500 |
| 2 | 200 | 1000 | 1000 | 1000 | 1000 | 960 |
| 3 | -100 | 700 | 1500 | 1500 | 1500 | |
| 4 | 400 | 1200 | 2000 | 2000 | ||
| 5 | 100 | 900 | 1700 | 2500 |
(解答本题第⑴小题只需在下面的表格的空位中填入你认为正确的数据即可)
查看习题详情和答案>>已知函数
(1)若函数 的图象经过P(3,4)点,求a的值;
的图象经过P(3,4)点,求a的值;
(2)比较 大小,并写出比较过程;
大小,并写出比较过程;
(3)若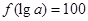 ,求a的值.
,求a的值.
【解析】本试题主要考查了指数函数的性质的运用。第一问中,因为函数 的图象经过P(3,4)点,所以
的图象经过P(3,4)点,所以 ,解得
,解得 ,因为
,因为 ,所以
,所以 .
.
(2)问中,对底数a进行分类讨论,利用单调性求解得到。
(3)中,由 知,
知, .,指对数互化得到
.,指对数互化得到 ,,所以
,,所以 ,解得所以,
,解得所以, 或
或  .
.
解:⑴∵函数 的图象经过
的图象经过 ∴
∴ ,即
,即 . … 2分
. … 2分
又 ,所以
,所以 .
………… 4分
.
………… 4分
⑵当 时,
时, ;
;
当 时,
时, . ……………… 6分
. ……………… 6分
因为, ,
,
当 时,
时, 在
在 上为增函数,∵
上为增函数,∵ ,∴
,∴ .
.
即 .当
.当 时,
时, 在
在 上为减函数,
上为减函数,
∵ ,∴
,∴ .即
.即 . …………………… 8分
. …………………… 8分
⑶由 知,
知, .所以,
.所以, (或
(或 ).
).
∴ .∴
.∴ , … 10分
, … 10分
∴ 或
或
 ,所以,
,所以, 或
或  .
.
查看习题详情和答案>>