网址:http://m.1010jiajiao.com/timu_id_316214[举报]
(本小题满分12分)已知直线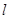 的参数方程为
的参数方程为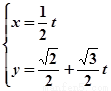 (
(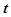 为参数),若以直角坐标系
为参数),若以直角坐标系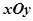 的
的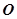 点为极点,
点为极点,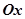 方向为极轴,选择相同的长度单位建立极坐标系,得曲线
方向为极轴,选择相同的长度单位建立极坐标系,得曲线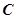 的极坐标方程为
的极坐标方程为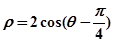
(1)将直线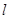 的参数方程化为普通方程,把曲线
的参数方程化为普通方程,把曲线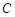 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)若直线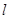 与曲线
与曲线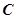 交于
交于 两点,求
两点,求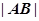 .
.
查看习题详情和答案>>
甲、乙两人独立地破译1个密码,他们能译出密码的概率分别为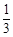 和
和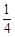 ,求(1)恰有1人译出密码的概率;
,求(1)恰有1人译出密码的概率;
(2)若达到译出密码的概率为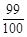 ,至少需要多少个乙这样的人?
,至少需要多少个乙这样的人?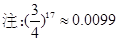
【解析】第一问中,考虑两种情况,是甲乙中的那个人译出密码,然后利用互斥事件概率公式相加得到。
第二问中,利用间接法n个乙这样的人都译不出密码的概率为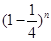 .可以得到结论。
.可以得到结论。
解:设“甲译出密码”为事件A;“乙译出密码”为事件B,则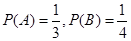 .
.
(1)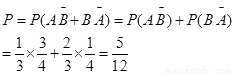 ………………5分
………………5分
(2)n个乙这样的人都译不出密码的概率为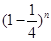 .
.
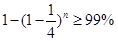 .解得.
.解得.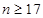
达到译出密码的概率为99/100,至少需要17人.
查看习题详情和答案>>
已知中心在原点,焦点在 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为 ,且经过点
,且经过点
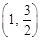 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)是否存过点 (2,1)的直线
(2,1)的直线 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点 ,满足
,满足 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
【解析】第一问利用设椭圆 的方程为
的方程为 ,由题意得
,由题意得
解得
第二问若存在直线 满足条件的方程为
满足条件的方程为 ,代入椭圆
,代入椭圆 的方程得
的方程得
 .
.
因为直线 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点 ,设
,设 两点的坐标分别为
两点的坐标分别为 ,
,
所以
所以 .解得。
.解得。
解:⑴设椭圆 的方程为
的方程为 ,由题意得
,由题意得
解得 ,故椭圆
,故椭圆 的方程为
的方程为 .……………………4分
.……………………4分
⑵若存在直线 满足条件的方程为
满足条件的方程为 ,代入椭圆
,代入椭圆 的方程得
的方程得
 .
.
因为直线 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点 ,设
,设 两点的坐标分别为
两点的坐标分别为 ,
,
所以
所以 .
.
又 ,
,
因为 ,即
,即 ,
,
所以
 .
.
即 .
.
所以 ,解得
,解得 .
.
因为A,B为不同的两点,所以k=1/2.
于是存在直线L1满足条件,其方程为y=1/2x
查看习题详情和答案>>
已知函数
(1)若函数 的图象经过P(3,4)点,求a的值;
的图象经过P(3,4)点,求a的值;
(2)比较 大小,并写出比较过程;
大小,并写出比较过程;
(3)若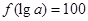 ,求a的值.
,求a的值.
【解析】本试题主要考查了指数函数的性质的运用。第一问中,因为函数 的图象经过P(3,4)点,所以
的图象经过P(3,4)点,所以 ,解得
,解得 ,因为
,因为 ,所以
,所以 .
.
(2)问中,对底数a进行分类讨论,利用单调性求解得到。
(3)中,由 知,
知, .,指对数互化得到
.,指对数互化得到 ,,所以
,,所以 ,解得所以,
,解得所以, 或
或  .
.
解:⑴∵函数 的图象经过
的图象经过 ∴
∴ ,即
,即 . … 2分
. … 2分
又 ,所以
,所以 .
………… 4分
.
………… 4分
⑵当 时,
时, ;
;
当 时,
时, . ……………… 6分
. ……………… 6分
因为, ,
,
当 时,
时, 在
在 上为增函数,∵
上为增函数,∵ ,∴
,∴ .
.
即 .当
.当 时,
时, 在
在 上为减函数,
上为减函数,
∵ ,∴
,∴ .即
.即 . …………………… 8分
. …………………… 8分
⑶由 知,
知, .所以,
.所以, (或
(或 ).
).
∴ .∴
.∴ , … 10分
, … 10分
∴ 或
或
 ,所以,
,所以, 或
或  .
.
查看习题详情和答案>>