摘要:折叠问题的计算与证明:一定要关注“变量 和“不变量 在证明和计算中的应用:折叠时位于棱同侧的位置关系和数量关系不变;位于棱两侧的位置关系与数量关系变.折前折后的图形结合起来使用.
网址:http://m.1010jiajiao.com/timu_id_4389727[举报]
某报对“男女同龄退休”这一公众关注的问题进行了民意调查,数据如下表
根据表中数据,能否认为对这一问题的看法与性别有关?
查看习题详情和答案>>
| 看法 性别 |
赞同 | 反对 | 合计 |
| 男 | 198 | 217 | 415 |
| 女 | 476 | 107 | 585 |
| 合计 | 674 | 326 | 1000 |
某媒体对“男女同龄退休”这一公众关注的问题进行 了民意调査,右表是在某单位得到的数据(人数):
(1 )能否有90%以上的把握认为对这一问题的看法与性别有关?
(2)进一步调查:(ⅰ)从赞同“男女同龄退休”16人中选出3人进行陈述发言,求事件“男士和女士各至少有1人发言”的概率;
(ⅱ)从反对“男女同龄退休”的9人中选出3人进行座谈,设参加调査的女士人数为X,求X的分布列和期望.
附表:
K2=
.
查看习题详情和答案>>
| 赞同 | 反对 | 合计 | |
| 男 | 5 | 6 | 11 |
| 女 | 11 | 3 | 14 |
| 合计 | 16 | 9 | 25 |
(2)进一步调查:(ⅰ)从赞同“男女同龄退休”16人中选出3人进行陈述发言,求事件“男士和女士各至少有1人发言”的概率;
(ⅱ)从反对“男女同龄退休”的9人中选出3人进行座谈,设参加调査的女士人数为X,求X的分布列和期望.
附表:
| P(K2≥K) | 0.25 | 0.15 | 0.10 |
| k | 1.323 | 2.072 | 2.706 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
(2012•河南模拟)某媒体对“男女同龄退休”这一公众关注的问题进行了民意调査,右表是在某单位得到的数据(人数):
(I )能否有90%以上的把握认为对这一问题的看法与性别有关?
(II)进一步调查:
(i )从赞同“男女同龄退休”16人中选出3人进行陈述发言,求事件“男士和女士各至少有1人发言”的概率;
(ii )从反对“男女同龄退休”的9人中选出3人进行座谈,设参加调査的女士人数为X,求X的分布列和均值.
附:
查看习题详情和答案>>
| 赞同 | 反对 | 合计 | |
| 男 | 5 | 6 | 11 |
| 女 | 11 | 3 | 14 |
| 合计 | 16 | 9 | 25 |
(II)进一步调查:
(i )从赞同“男女同龄退休”16人中选出3人进行陈述发言,求事件“男士和女士各至少有1人发言”的概率;
(ii )从反对“男女同龄退休”的9人中选出3人进行座谈,设参加调査的女士人数为X,求X的分布列和均值.
附:

某媒体对“男女同龄退佈”这一公众关注的问题进行了民意调査,右表是在某单位得到的数据(人数):
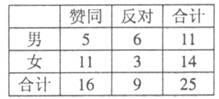
(I )能否有90%以上的把握认为对这一问题的看法与性别有关?
(II)进一步调查:
(i )从赞同“男女同龄退休” 16人中选出3人进行陈述发言,求事件“男士和女士各至少有1人发言”的概率;
(ii )从反对“男女同龄退休”的9人中选出3人进行座谈,设参加调査的女士人数为X,求X的分布列和均值.
附:
查看习题详情和答案>>
某媒体对“男女同龄退休”这一公众关注的问题进行 了民意调査,右表是在某单位得到的数据(人数):
(1 )能否有90%以上的把握认为对这一问题的看法与性别有关?
(2)进一步调查:(ⅰ)从赞同“男女同龄退休”16人中选出3人进行陈述发言,求事件“男士和女士各至少有1人发言”的概率;
(ⅱ)从反对“男女同龄退休”的9人中选出3人进行座谈,设参加调査的女士人数为X,求X的分布列和期望.
附表:
 .
.
查看习题详情和答案>>
| 赞同 | 反对 | 合计 | |
| 男 | 5 | 6 | 11 |
| 女 | 11 | 3 | 14 |
| 合计 | 16 | 9 | 25 |
(2)进一步调查:(ⅰ)从赞同“男女同龄退休”16人中选出3人进行陈述发言,求事件“男士和女士各至少有1人发言”的概率;
(ⅱ)从反对“男女同龄退休”的9人中选出3人进行座谈,设参加调査的女士人数为X,求X的分布列和期望.
附表:
| P(K2≥K) | 0.25 | 0.15 | 0.10 |
| k | 1.323 | 2.072 | 2.706 |
 .
.查看习题详情和答案>>