摘要:问题1.(辽宁)棱长为的正方体.连结相邻面的中心.以这些线段为棱的 八面体的体积为 已知一个正四面体和一个正八面体的棱长相等且为.把它们拼起来.使一个表面重合.所得的多面体有多少个面? 问题2.(天津)一个长方体的各顶点均在同一球的球面上.且一个顶点上的三条棱的长分别为.则此球的表面积为 (全国Ⅰ文)正四棱锥的底面边长和各侧棱长都为.点 都在同一个球面上.则该球的体积为 (江西文)四面体的外接球球心在上.且.. 在外接球面上两点.间的球面距离是 (陕西)水平桌面上放有个半径均为的球.且相邻的球都相切.在这个球的上面放个半径为的小球.它和下面个球恰好都相切.则小球的球心到水平桌面的距离是 问题3. (四川)设球的半径是...是球面上三点.已知到.两点的球面距离都是.且二面角的大小为.则从点沿球面经.两点再回到点的最短距离是 问题4.三棱锥的两条棱.其余各棱长均为.求三棱锥的内切球半径和外接球半径. 问题5.已知球的半径为.在球内作一个内接圆柱.这个圆柱底面半径与高为何值时.它的侧面积最大?侧面积的最大值是多少?
网址:http://m.1010jiajiao.com/timu_id_4389724[举报]
求复杂区域的体积往往需要经历将其分割后求其各部分的体积,最后再求和的过程.试运用此思想考虑如下问题:在一个棱长为6 cm的正方体盒子中,放一个半径为1 cm的小球,任意摇动盒子,问:
(1)盒子内的哪些空间小球不能到达?
(2)你能求出小球不能到达的空间的体积吗?
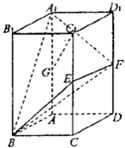 如图,正四棱柱ABCD-A1B1C1D1的底面边长为1,侧棱长为2,E、F、G分别CC1、DD1、AA1中点.
如图,正四棱柱ABCD-A1B1C1D1的底面边长为1,侧棱长为2,E、F、G分别CC1、DD1、AA1中点.