 已知函数
已知函数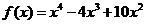 ,则方程
,则方程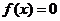 在区间
在区间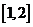 上的根有
上的根有

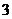 个
个

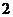 个
个

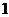 个
个 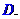
 个
个
 (
( 郑州一中等四校联考)若函数
郑州一中等四校联考)若函数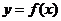 在
在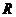 上可导且满足不等式
上可导且满足不等式
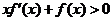 恒成立,且常数
恒成立,且常数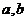 满足
满足 ,则下列不等式一定成立的是
,则下列不等式一定成立的是

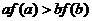

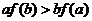

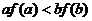

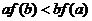
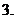 求满足条件的
求满足条件的 的范围:
的范围:
 使
使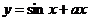 为
为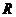 上增函数,则
上增函数,则 的范围是
的范围是
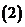 使
使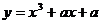 为
为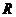 上增函数,则
上增函数,则 的范围是
的范围是
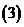 使
使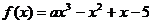 为
为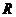 上增函数,则
上增函数,则 的范围是
的范围是
 证明方程
证明方程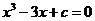 在
在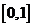 上至多有一实根.
上至多有一实根.
 (
( 届高三陕师大附中八模)如果
届高三陕师大附中八模)如果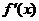 是二次函数, 且
是二次函数, 且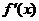 的图象开口向上,
的图象开口向上,
顶点坐标为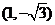 , 那么曲线
, 那么曲线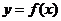 上任一点的切线的倾斜角
上任一点的切线的倾斜角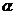 的取值范围是
的取值范围是

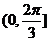



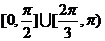

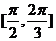
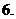 (
( 届厦门双十中学高三月考)如图,是函数
届厦门双十中学高三月考)如图,是函数
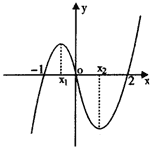
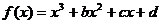 的大致图像,
的大致图像,
|
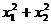 等于
等于

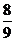

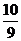

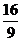


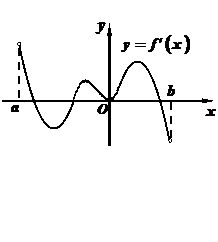
 (
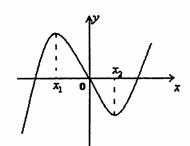
(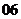 天津)函数
天津)函数 的定义域是开区间
的定义域是开区间 ,
,
导函数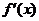 在
在 内的图象如图所示,则函数
内的图象如图所示,则函数
 在开区间内有极小值点
在开区间内有极小值点
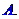
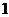 个
个 
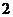 个
个 
 个
个 
 个
个
 (
( 届高三哈尔滨第三中学第一次月考)
届高三哈尔滨第三中学第一次月考)
函数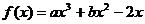 的图象如图所示,
的图象如图所示,
且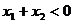 ,则有
,则有

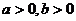

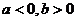

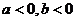

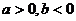
 已知:
已知: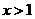 ,证明不等式:
,证明不等式: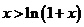
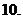 设
设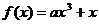 恰有三个单调区间,试确定
恰有三个单调区间,试确定 的取值范围,并求出这三个单调区间
的取值范围,并求出这三个单调区间
 (
( 届高三福建质检)已知函数
届高三福建质检)已知函数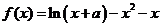 在
在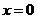 处取得极值.
处取得极值.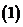 求实数
求实数 的值;
的值;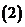 若关于
若关于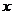 的方程
的方程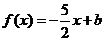 在区间
在区间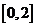 上恰有两个不同的实数根,求实数
上恰有两个不同的实数根,求实数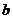 的取值范围;
的取值范围;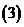 证明:对任意的正整数
证明:对任意的正整数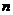 ,不等式
,不等式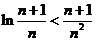 都成立.
都成立.
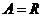 ,
,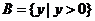 ,
,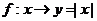 ;
;
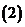
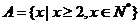 ,
,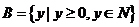 ,
, ;
;
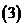
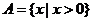 ,
,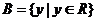 ,
,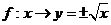 .
.
上述三个对应
是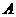 到
到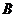 的映射.
的映射.
 给定映射
给定映射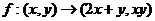 ,点
,点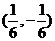 的原象是
的原象是
 下列函数中,与函数
下列函数中,与函数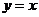 相同的函数是
相同的函数是

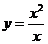

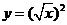

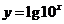

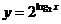
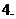 设函数
设函数 ,则
,则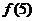 =
=
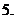 (
(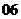 湖北八校一联)设
湖北八校一联)设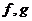 都是由
都是由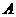 到
到 的映射,其对应法则如下表(从上到下):
的映射,其对应法则如下表(从上到下):
表一 映射 的对应法则
表二 映射
的对应法则
表二 映射 的对应法则
的对应法则
|
原象 |
 |
 |
 |
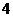 |
|
象 |
 |
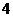 |
 |
 |
|
原象 |
 |
 |
 |
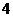 |
|
象 |
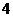 |
 |
 |
 |
则与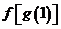 相同的是
相同的是 
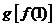

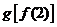

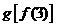

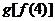
 (
( 灌云模拟)设
灌云模拟)设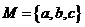 ,从
,从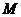 到
到 的映射
的映射 满足
满足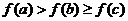 ,
,
试确定这样的映射 的个数为
的个数为 






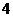
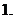 函数解析式的求解;
函数解析式的求解;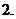 函数定义域的求解.
函数定义域的求解.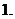 (
( 全国Ⅰ)设
全国Ⅰ)设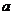 是实数,且
是实数,且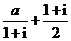 是实数,则
是实数,则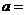

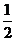

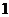

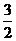

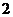
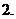 (
(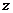 满足
满足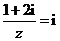 ,则
,则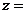
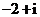

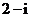
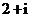
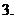 (
(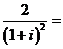
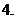 (
(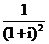 等于
等于 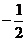
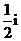
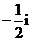
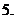 (
(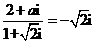 ,则
,则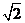
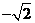
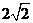
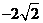
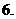 (
(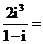
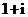
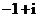
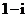
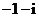
 (
(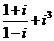 的值是
的值是
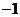
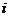
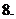 (
(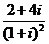 的结果是
的结果是 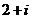
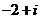
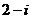
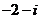
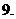 (
(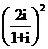 等于
等于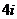
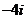
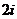
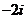
 (
(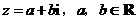 ,且
,且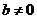 ,若
,若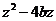 是实数,则有序实数对
是实数,则有序实数对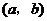 可以是
(写出一个有序实数对即可)
可以是
(写出一个有序实数对即可)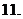 (
(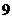 )对于非零实数
)对于非零实数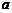 、
、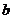 ,以下四个命题都成立:
,以下四个命题都成立: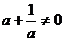 ;
②
;
② 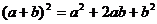 ;
; 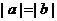 ,则
,则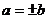 ; ④ 若
; ④ 若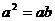 ,则
,则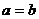 .
.  (
( 的虚部为
的虚部为
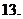 (
(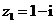 ,
,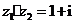 ,则复数
,则复数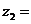
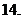 (
(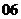 上海)若复数
上海)若复数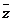 =
=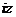 (
(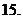 (
(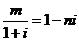 ,其中
,其中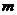 、
、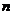 是实数,
是实数,
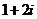
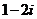
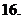 (
(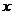 、
、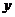 为实数,且
为实数,且 ,则
,则
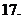 (
(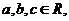 则复数
则复数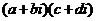 为实数的充要条件是( )
为实数的充要条件是( )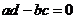
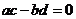
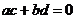
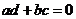
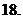 (
(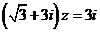 ,则
,则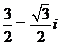
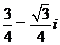
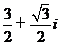
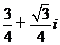
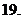 (
(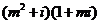 是实数,则实数
是实数,则实数
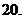 (
(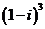 的虚部为
的虚部为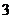
 .
. 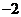
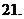 (
(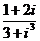 的值是
的值是
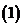 它的平方等于
它的平方等于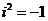 ;
; 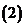 实数可以与它进行四则运算,进行四则运算时,原有加、乘运算律仍然成立.
实数可以与它进行四则运算,进行四则运算时,原有加、乘运算律仍然成立.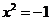 的一个根,方程
的一个根,方程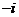 .
.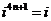 ,
, 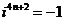 ,
,  ,
,  .
.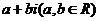 的数叫复数,
的数叫复数,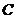 表示
表示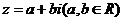 ,把复数表示成
,把复数表示成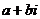 的形式,叫做复数的代数形式.
的形式,叫做复数的代数形式.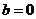 时,复数
时,复数 叫做虚数;当
叫做虚数;当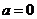 且
且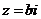 叫做纯虚数;当且仅当
叫做纯虚数;当且仅当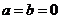 时,
时,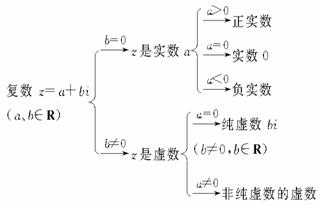
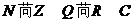
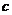 ,
,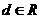 ,那么
,那么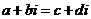
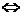
 ,
,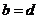
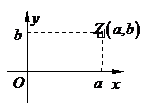
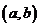 是一一对应关系.建立一一对应的关系.点
是一一对应关系.建立一一对应的关系.点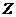 的横坐标是
的横坐标是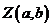 表示,这个
表示,这个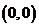 , 它所确定的复数是
, 它所确定的复数是 表示是实数.故除了原点外,虚轴上的点都表示纯虚数.
表示是实数.故除了原点外,虚轴上的点都表示纯虚数. 复平面内的点
复平面内的点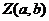
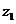 与
与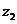 的和的定义:
的和的定义: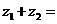
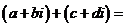
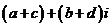
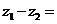
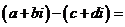
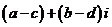
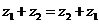
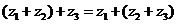
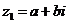 ,
,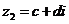 (
(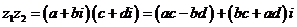
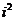 换成
换成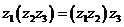
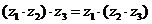
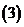
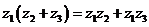
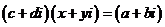 的复数
的复数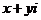 (
(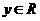 )叫复数
)叫复数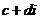 的商,记为:
的商,记为: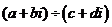 或者
或者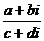
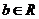 ),除以
),除以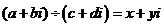 ∵
∵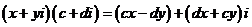
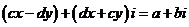
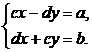 解这个方程组,得
解这个方程组,得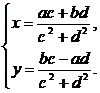
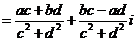
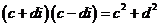 于是将
于是将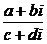 的分母有理化得:
的分母有理化得: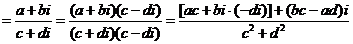
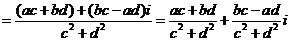 .
.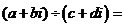
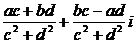
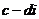 ,相当于我们初中学习的
,相当于我们初中学习的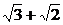 的对偶式
的对偶式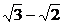 ,它们之积为
,它们之积为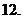 (
(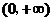 上的非负可导函数,且满足
上的非负可导函数,且满足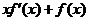 ≤
≤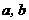 ,若
,若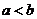 ,则必有
,则必有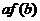 ≤
≤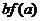
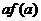 ≤
≤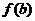
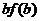 ≤
≤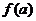
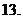 (
( 的导数为
的导数为 ,对于任意实数
,对于任意实数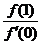 的最小值为
的最小值为 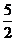
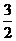
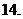 (
(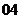 全国)函数
全国)函数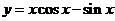 在下面哪个区间内是增函数
在下面哪个区间内是增函数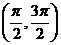
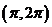
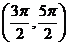
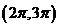
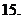 (
( 重庆)曲线
重庆)曲线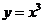 在点
在点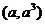
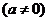 处的切线与
处的切线与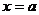 所围成的三角形的面积为
所围成的三角形的面积为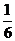 ,则
,则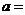
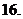 (
(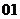 全国)已知
全国)已知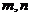 是正整数且
是正整数且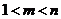 ,求证:
,求证: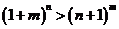
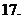 (
(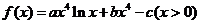 在
在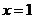 处取得极值
处取得极值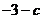 ,其中
,其中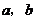 为常数.(Ⅰ)试确定
为常数.(Ⅰ)试确定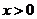 ,不等式
,不等式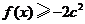 恒成立,求
恒成立,求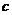 的取值范围.
的取值范围.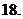 (
(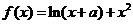
 时,
时,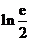 .
.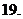 (
(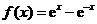 .
.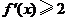 ;
;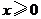 都有
都有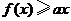 ,求
,求 (
(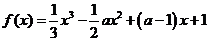 在区间
在区间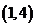 内为减函数,在区间
内为减函数,在区间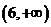 内为增函数,试求实数
内为增函数,试求实数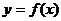 在定义域
在定义域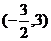 内可导,其图象如图所示,记
内可导,其图象如图所示,记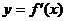 ,则不等式
,则不等式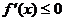 的解集为
的解集为 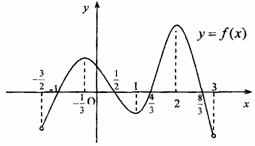

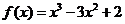 ,
,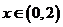 的反函数为
的反函数为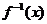 ,则
,则 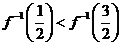
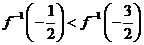
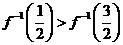

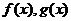 均是定义在
均是定义在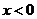 时,
时,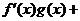
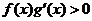 ,且
,且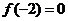 ,则不等式
,则不等式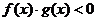 的解集是
的解集是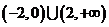
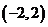
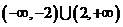
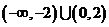
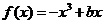 在区间
在区间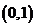 上单调递增,并且方程
上单调递增,并且方程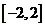 内,则
内,则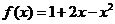 ,那么
,那么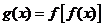
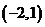 上单调递增
上单调递增 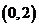 上单调递增
上单调递增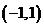 上单调递增
上单调递增
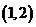 上单调递增
上单调递增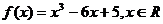 ,
,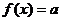 有
有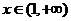 时,
时,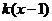 恒成立,求实数
恒成立,求实数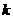 的取值范围.
的取值范围.
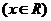 ,其中
,其中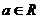 .
.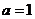 时,求曲线
时,求曲线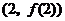 处的切线方程;
处的切线方程; 时,求函数
时,求函数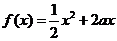 ,
, ,其中
,其中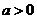 .设两曲线
.设两曲线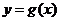 有公共点,且在该点处的切线相同.(Ⅰ)用
有公共点,且在该点处的切线相同.(Ⅰ)用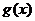 (
( (
(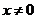 ,
, 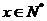 ).
).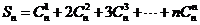 (
(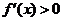 在
在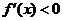 在
在
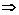
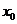 附近有定义,如果对
附近有定义,如果对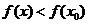 ,就说
,就说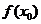 是函数
是函数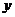 极大值
极大值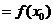 ,
,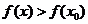 就说
就说
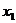 是极大值点,
是极大值点,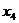 是极小值点,而
是极小值点,而 >
>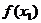 .
.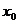 满足
满足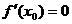 ,且在
,且在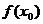 是极值,并且如果
是极值,并且如果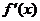 在
在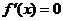 的根
的根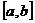 上连续的函数
上连续的函数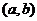 内连续的函数
内连续的函数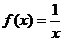 在
在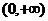 内连续,但没有最大值与最小值;
内连续,但没有最大值与最小值;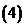 函数在其定义区间上的最大值、最小值最多各有一个,而函数的极值可能不止一个,也可能没有一个.
函数在其定义区间上的最大值、最小值最多各有一个,而函数的极值可能不止一个,也可能没有一个.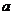 、
、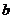 、
、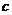 、
、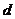 对应密文
对应密文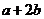 ,
,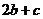 ,
,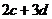 ,
,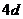 .例如:明文
.例如:明文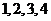 对应密文
对应密文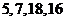 .当接收方收到密文
.当接收方收到密文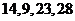 时,则解密得到的明文为
时,则解密得到的明文为 
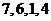


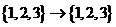 满足
满足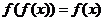 ,则这样的函数个数
,则这样的函数个数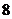 个
个 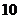 个
个 和
和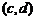 ,规定:
,规定: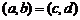 ,
,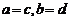 ;运算“
;运算“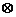 ”为:
”为: ;
;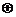 ”为:
”为: ,设
,设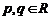 ,若
,若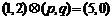 ,
,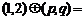

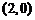
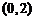
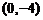
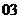 全国)已知
全国)已知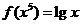 ,则
,则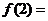 (
)
(
)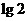
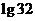
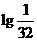
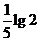
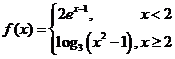 ,则
,则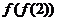 的值为
的值为
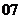 北京)已知函数
北京)已知函数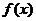 ,
, 分别由下表给出:
分别由下表给出: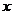
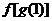 的值为 ;满足
的值为 ;满足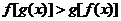 的
的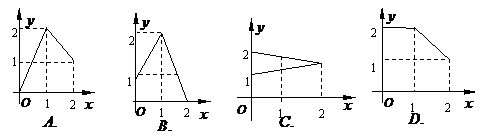 设
设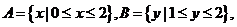 在下图中,能表示从集合
在下图中,能表示从集合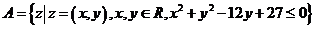 到集合
到集合 的映射
的映射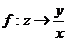 ,则该映射的象集为
,则该映射的象集为
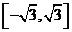
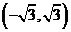
 北京东城模拟)设映射
北京东城模拟)设映射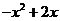 是实数集
是实数集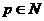 ,在
,在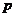 的取值范围是
的取值范围是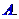
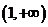
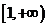
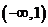
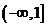
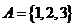 ,
,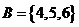 ,定义映射
,定义映射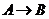 ,使对任意
,使对任意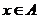 ,都有
,都有 是奇数,则这样的映射
是奇数,则这样的映射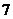
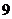
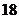
 ,则
,则 )
)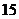
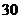
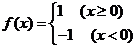 ,则不等式
,则不等式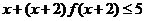 的解集是
的解集是
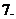 设
设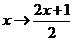 是
是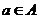 ,则
,则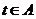 ,那么
,那么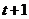 在
在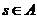 ,若
,若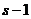 在映射
在映射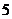 ,则
,则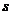 应是多少?
应是多少?