2、对数函数的性质:
|
|
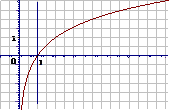
a>1 |
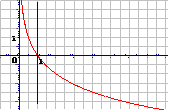
0<a<1 |
|
图 象 |
 |
 |
|
性 质 |
定义域:(0,+∞) |
|
值域:R |
||
过点(1,0),即当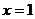 时, 时,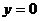  |
||
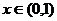 时 时 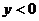  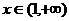 时 时 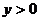  |
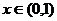 时 时 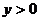  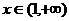 时 时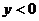  |
|
在(0,+∞)上是增函数 |
在(0,+∞)上是减函数 |
2、对数函数的性质:
|
|
a>1 |
0<a<1 |
|
图 象 |
 |
 |
|
性 质 |
定义域:(0,+∞) |
|
值域:R |
||
过点(1,0),即当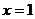 时, 时,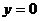  |
||
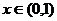 时 时 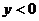  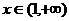 时 时 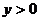  |
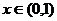 时 时 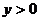  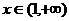 时 时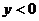  |
|
在(0,+∞)上是增函数 |
在(0,+∞)上是减函数 |