16、某工程机械厂根据市场需求,计划生产A、B两种型号的大型挖掘机共100台,该厂所筹生产资金不少于22400万元,但不超过22500万元,且所筹资金全部用于生产此两型挖掘机,所生产的此两型挖掘机可全部售出,此两型挖掘机的生产成本和售价如下表:
|
型号 |
A |
B |
|
成本(万元/台) |
200 |
240 |
|
售价(万元/台) |
250 |
300 |
(1)该厂对这两型挖掘机有哪几种生产方案?
(2)该厂如何生产能获得最大利润?
(3)根据市场调查,每台B型挖掘机的售价不会改变,每台A型挖掘机的售价将会提高m万元(m>0),该厂应该如何生产可以获得最大利润?(注:利润=售价-成本)
命题意图:考查学生解决实际问题的能力,试题的特色是在要求学生能读懂题意,并且会用函数知识去解题,以及会讨论函数的最大值。
参考答案:(1) 设生产A种型号的大型挖掘机x台,则生产B种型号的大型挖掘机(100-x)台。
则22400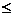 200x+240(100-x)
200x+240(100-x) 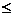 22500
22500
解得:37.5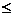 x
x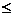 40
40
X可以取38、39、40
(2) 设最大利润是w元
则w=50x+60(100-x)=6000-10x,当x=38 时,w有最大值。
(3) 因为w=(50+m)x+60(100-x)=6000+( m-10)x
则当0<m<10,x=38, w最大
当m=10,三个方案都一样。
当m>10,x=40, w最大.
试题来源:2007年山东省临沂市初中毕业与高中招生考试
14、灌云县实验中学为了解毕业年级800名学生每学期参加社会实践活动的时间,随机对该年级60名学生每学期参加社会实践活动的时间进行了统计,结果如下表:
|
时间/天 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
人数 |
3 |
3 |
5 |
7 |
8 |
13 |
8 |
7 |
4 |
2 |
|
分组 |
频数 |
频率 |
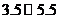 |
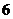 |
 |
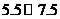 |
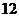 |
 |
 |
|
|
 |
|
|
 |
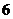 |
 |
|
合计 |
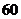 |
 |
(1)补全右面的频率分布表;
(2)请你估算这所学校该年级的学生中,每学期参加社会实践活动的时间大于7天的约有多少人?
命题意图:考查学生对于统计知识的掌握,试题的特色是与学生平时的生活密切相关。
参考答案:(1) ,
,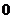 ,
,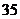 ;
; ,
,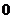 ,
,
(2)
试题来源:2007年泰安市中等学校招生考试
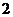 ,母线长为
,母线长为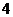 ,则它的侧面积为( )
,则它的侧面积为( ) B.
B.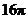 C.
C.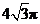 D.
D.
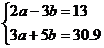 的解是
的解是 ,则方程组
,则方程组 的解是( )
的解是( )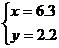 B.
B. C.
C.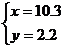 D.
D.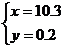

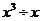 的结果是( )
的结果是( ) 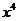 B.
B. C.
C.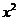 D.
D.
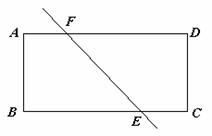 (1)求出直线EE′分别经过原矩形的顶点A和顶点D时,所对应的 x:b的值;
(1)求出直线EE′分别经过原矩形的顶点A和顶点D时,所对应的 x:b的值;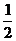 a(x+AF)=
a(x+AF)= (Ⅱ)(1)当直线EE′经过原矩形的顶点D时,如图(一),
(Ⅱ)(1)当直线EE′经过原矩形的顶点D时,如图(一), =
= .
.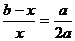 ,
, ;
;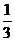 .
. 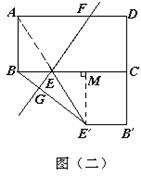 ∴∠GBE=∠ME′E.
∴∠GBE=∠ME′E. =
= .
.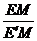 =
=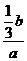 ,
,
 ,
,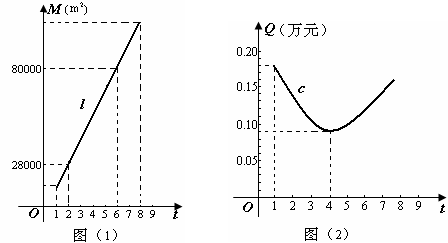
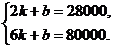

 知,当t=1时,S用地面积=M建筑面积,
知,当t=1时,S用地面积=M建筑面积,


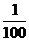 ( t-4)2+
( t-4)2+ ,
, t +
t + , 1≤t≤8.
, 1≤t≤8.  (元);
(元);  ⑵ ∵11.875元>10元,
⑵ ∵11.875元>10元,