7.在演示光电效应的实验中,把某种金属板连在验电器上,第一次,用弧光灯直接照射金属板,验电器的指针就张开一个角度。第二次,在弧光灯和金属板之间,插入一块普通玻璃板,再用弧光灯照射,验电器指针不张开。由此可以判定,使金属板产生光电效应的是弧光中的 ( )
A.可见光成份 B.红外光成份 C.紫外光成份 D.无线电波成份
 8.如图所示,粗细均匀的U形管,左管封闭一段空气柱,两侧
8.如图所示,粗细均匀的U形管,左管封闭一段空气柱,两侧
水银面高度差为h,U形管两管间宽度为d,且d<h。现将
U形管以O点为轴顺时针旋转90°,至两平行管水平,并保
持U形管在竖直面内。设温度不变,管的直径可忽略不计,
水银没有溢出,则下列说法中正确的是 ( )
A.封闭端水银柱的长度h1增大,开口端水银柱的长度h2减小,
静止时h1>h2,封闭气体压强增大
B.封闭端水银柱的长度h1减小,开口端水银柱的长度h2增大,静止时h1=h2,封闭
气体压强不变
C.封闭端水银柱的长度h1减小,开口端水银柱的长度h2增大,静止时h1>h2,封闭气体压强增大
D.封闭端水银柱的长度h1减小,开口端水银柱的长度h2增大,静止时h1<h2,封闭气体压强减小
 9.一弹簧振子做简谐运动,其振动图像如图所示,那么在(
9.一弹簧振子做简谐运动,其振动图像如图所示,那么在(
-Dt)和(+Dt)(Dt是微小的时间)两时刻,振子的:
①速度相同;
②加速度相同;
③相对平衡位置的位移相同;
④振动的能量相同。以上选项中正确的是 ( )
A.①② B.②③ C.③④ D.①④
 10.两个所受重力大小分别为GA和GB的小球A和B,用轻杆
10.两个所受重力大小分别为GA和GB的小球A和B,用轻杆
连接,放置在光滑的半球形碗内。小球A、B与碗的球心
O在同一竖直平面内,如图所示,若碗的半径为R,细杆
的长度为R,GA>GB,由关于连接两小球的细杆AB静
|
A.arctan+ B.arctan+
C.-arctan D.-arctan
 三、(20分)多项选择题。本大题共4小题,每小题5分,每小题给出的四个选项中,有二个或二个以上是正确的。把正确答案全选出来,并将正确答案前面的字母填写在答题纸上。每一小题全选对的得5分;选对但不全,得部分分;有选错或不答的,得0分。填写在方括号外的字母,不作为选出的答案。
三、(20分)多项选择题。本大题共4小题,每小题5分,每小题给出的四个选项中,有二个或二个以上是正确的。把正确答案全选出来,并将正确答案前面的字母填写在答题纸上。每一小题全选对的得5分;选对但不全,得部分分;有选错或不答的,得0分。填写在方括号外的字母,不作为选出的答案。
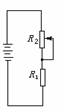 1A.法国科学家拉普拉斯曾说过:“认识一位巨人的研究方法对于科学的进步并不比发现本身有更少的用处……”。在物理学的重大发现中科学家们创造出了许多物理学方法,如观察、实验、建立模型、物理类比和物理假说等方法。其中物理假说,是根据一定的科学事实和科学理论对研究的问题提出假说性的看法或说明,例如麦克斯韦的电磁场理论、分子动理论等假说,请你再举出两个物理假说的例子____ ______;__
__。
1A.法国科学家拉普拉斯曾说过:“认识一位巨人的研究方法对于科学的进步并不比发现本身有更少的用处……”。在物理学的重大发现中科学家们创造出了许多物理学方法,如观察、实验、建立模型、物理类比和物理假说等方法。其中物理假说,是根据一定的科学事实和科学理论对研究的问题提出假说性的看法或说明,例如麦克斯韦的电磁场理论、分子动理论等假说,请你再举出两个物理假说的例子____ ______;__
__。  3A.如图所示,边长为L的正方形区域abcd内存在着匀强电场,
3A.如图所示,边长为L的正方形区域abcd内存在着匀强电场, B类题(适合于使用二期课改教材的考生)
B类题(适合于使用二期课改教材的考生)
 3B.如图所示,边长为L的正方形区域abcd内存在着匀强
3B.如图所示,边长为L的正方形区域abcd内存在着匀强 ______________。
______________。 4.一光滑圆环固定在竖直平面内,环上套着两个小球A和
4.一光滑圆环固定在竖直平面内,环上套着两个小球A和 的拉力为___________,A球的质量为_____________。
的拉力为___________,A球的质量为_____________。
 =
=
 =
=



 tanα+tanβ+tanγ=tanαtanβtanγ
tanα+tanβ+tanγ=tanαtanβtanγ
 π+α)+cos(
π+α)+cos( +α)]+cos[kπ-(
+α)]+cos[kπ-( sinα
sinα ,cos(α-β)=
,cos(α-β)= 的值
的值

 解之得
解之得 ),x∈R,(其中A>0,ω>0)的图象在y轴右侧的第一个最高点(函数取最大值的点)为M(2,2
),x∈R,(其中A>0,ω>0)的图象在y轴右侧的第一个最高点(函数取最大值的点)为M(2,2 ),与x轴在原点右侧的第一个交点为N(6,0),求这个函数的解析式
),与x轴在原点右侧的第一个交点为N(6,0),求这个函数的解析式 =6-2=4
=6-2=4


 ,tanαcotα=1,以及正弦、余弦诱导公式
,tanαcotα=1,以及正弦、余弦诱导公式
 ±α,
±α, ±α与α角三角函数间的关系
±α与α角三角函数间的关系 .记该参赛者闯三关所得总分为
.记该参赛者闯三关所得总分为 .
.





 中,
中, ,
, ,
, ,
, 是棱
是棱 的中点.
的中点.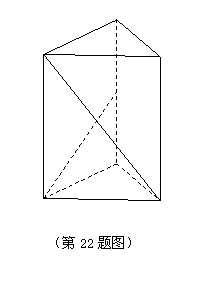 (1)求证:
(1)求证: ;
; 与平面
与平面 所成角的正弦值.
所成角的正弦值.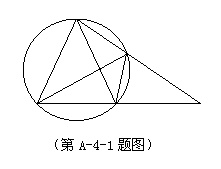 如图,
如图, 是等腰三角形
是等腰三角形 的外接圆,
的外接圆, ,延长
,延长 到点
到点 ,使
,使 ,连接
,连接 交
交 ,直线
,直线 交
交 于点
于点 .
. ,其中
,其中 ,若点
,若点 在矩阵
在矩阵 .
.  的值;
的值; 的参数方程为
的参数方程为
 ,曲线
,曲线 .
. 均为正实数,求证:
均为正实数,求证: .
.