0 52210 52218 52224 52228 52234 52236 52240 52246 52248 52254 52260 52264 52266 52270 52276 52278 52284 52288 52290 52294 52296 52300 52302 52304 52305 52306 52308 52309 52310 52312 52314 52318 52320 52324 52326 52330 52336 52338 52344 52348 52350 52354 52360 52366 52368 52374 52378 52380 52386 52390 52396 52404 447348
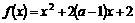 在区间
在区间 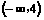 上是
上是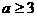 B.
B.
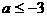 C.
C.
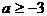 D.
D.
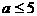
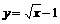 (x≥0)的反函数是
(
A )
(x≥0)的反函数是
(
A )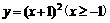 (B)y=
(B)y=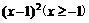
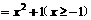 (C)y
(C)y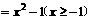
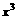 +a且f(-1)=0,则
+a且f(-1)=0,则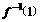 的值是 ( A
)
的值是 ( A
)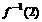 的值是
(
A )
的值是
(
A )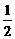 (B)
(B)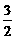 (C)
(C)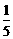 (D)5
(D)5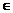
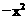 +1,则当x
+1,则当x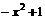 (B)
(B)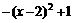
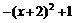 (D)
(D)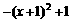

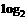 (x+1),
(x+1),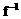 (1)=
。(1)
(1)=
。(1)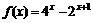 ,则
,则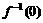 = 1 。
= 1 。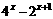 =0,解得
=0,解得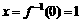
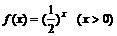 和定义在R上的奇函数
和定义在R上的奇函数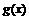 ,当x>0时,
,当x>0时,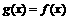 ,试求
,试求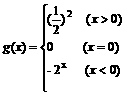
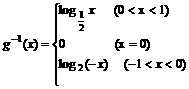
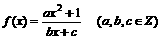 是奇函数,又
是奇函数,又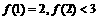 ,求a、b、c的整数值。
,求a、b、c的整数值。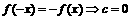 ,又由
,又由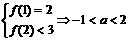 ,从而可得a=b=1;c=0
,从而可得a=b=1;c=0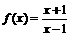 ,求
,求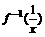
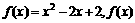 在
在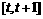 上的最小值为
上的最小值为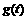 ;试写出
;试写出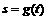 的解析式。
的解析式。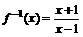 ,
,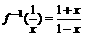 (
(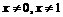 )
)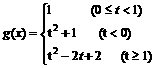
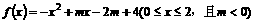 ,若
,若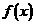 的最大值为n,求
的最大值为n,求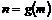 的表达式。
的表达式。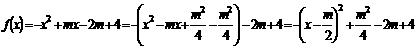

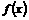 是R上的偶函数,且在区间
是R上的偶函数,且在区间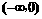 上递增,若
上递增,若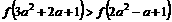 成立,求a的取值范围。
成立,求a的取值范围。
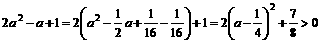
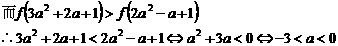
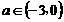 为所求。
为所求。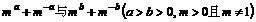 的大小。
的大小。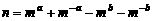
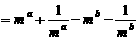
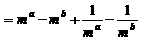
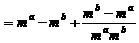
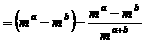
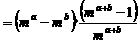
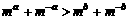 。
。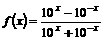 。(1)证明
。(1)证明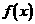 在
在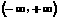 上是增函数;(2)求
上是增函数;(2)求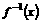 及其
及其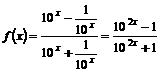
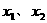 ,且
,且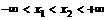
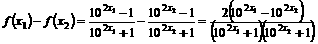
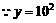 是增函数,
是增函数,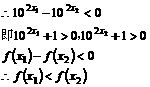

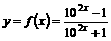 ;定义域R,值域(-1, 1)
;定义域R,值域(-1, 1)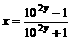
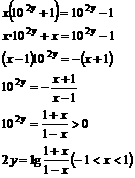
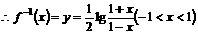
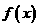 满足:对任意实数
满足:对任意实数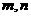 ,总有
,总有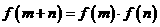 ,且当
,且当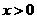 时,
时,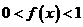 .
.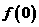 的值;
的值;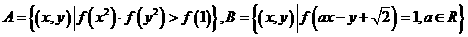 ,若
,若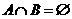 ,试确定
,试确定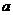 的取值范围.
的取值范围.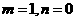 .得:
.得: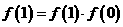 .
.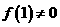 ,所以,
,所以,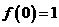 .
.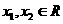 ,且设
,且设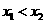 .
.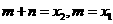 ,则已知条件可化为:
,则已知条件可化为: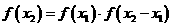 .
.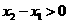 ,所以
,所以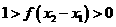 .
.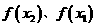 的大小,只需考虑
的大小,只需考虑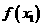 的正负即可.
的正负即可.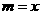 ,
,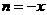 ,则得
,则得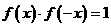 .
.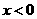 时,
时,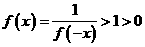 .
.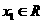 ,均有
,均有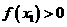 .
.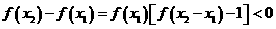 .
.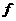 的式子.
的式子.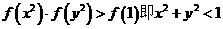 ,
,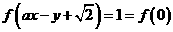 ,即
,即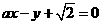 .
.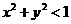 无公共点.所以,
无公共点.所以,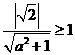 .
.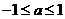 .
. .
.