0 52212 52220 52226 52230 52236 52238 52242 52248 52250 52256 52262 52266 52268 52272 52278 52280 52286 52290 52292 52296 52298 52302 52304 52306 52307 52308 52310 52311 52312 52314 52316 52320 52322 52326 52328 52332 52338 52340 52346 52350 52352 52356 52362 52368 52370 52376 52380 52382 52388 52392 52398 52406 447348
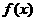 是定义在R上的以3为周期的奇函数,且
是定义在R上的以3为周期的奇函数,且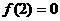 则方程
则方程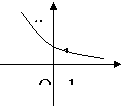 (2005年高考·福建卷·理5文6)函数
(2005年高考·福建卷·理5文6)函数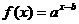 的图象如图,其中a、b为常数,则下列结论正确的是 ( D )
的图象如图,其中a、b为常数,则下列结论正确的是 ( D )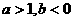 B.
B.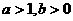
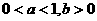 D.
D.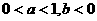
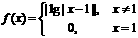 ,则关于
,则关于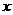 的方程
的方程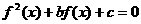 有7个不同实数解的充要条件是 ( C )
有7个不同实数解的充要条件是 ( C )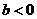 且
且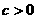 B.
B.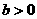 且
且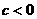 C.
C.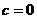 D.
D.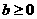 且
且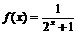 ,则该函数在
,则该函数在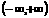 上是 ( A )
上是 ( A )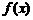 的定义域为
的定义域为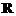 ,有下列三个命题:
,有下列三个命题: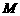 ,使得对任意
,使得对任意 ,有
,有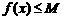 ,则
,则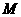 是函数
是函数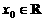 ,使得对任意
,使得对任意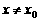 ,有
,有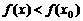 ,则
,则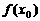 是函数
是函数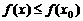 ,则
,则
 (2005年春考·北京卷·文2)函数
(2005年春考·北京卷·文2)函数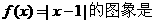 ( B )
( B )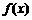 是定义在
是定义在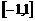 上的奇函数,
上的奇函数,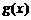 的图象与
的图象与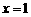 对称,而当
对称,而当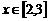 时,
时,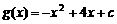 (c为常数)。
(c为常数)。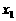 ,
,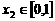 且
且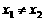 ,求证:
,求证: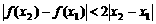 ;
;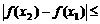 1.
1.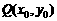 与f(x)上点P(x,y)对应,
与f(x)上点P(x,y)对应,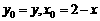 ;∵
;∵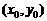 在g(x)图象上
在g(x)图象上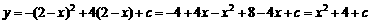
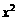
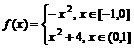
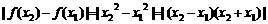
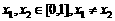 ,∴
,∴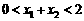 ,所以
,所以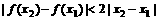
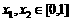 ,∴
,∴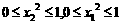
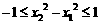 ,∴
,∴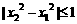
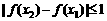
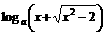 (a>0, a≠1)
(a>0, a≠1)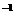 (x),并求出其定义域。
(x),并求出其定义域。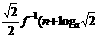 ),如果P(n)<
),如果P(n)<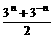 (n∈N),求a的取值范围。
(n∈N),求a的取值范围。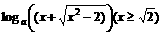
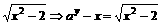
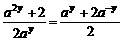
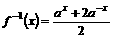 ∵a>1时,f(x)=
∵a>1时,f(x)=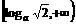
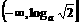
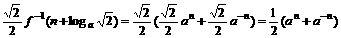
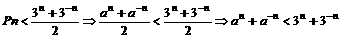
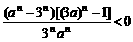
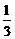 <a<3;
<a<3;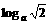 >
>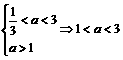
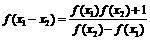 ②存在正常数a,使f(a) = 1,求证:(1)f(x)为奇函数;(2)f(x)为周期函数,且一个周期为4a。
②存在正常数a,使f(a) = 1,求证:(1)f(x)为奇函数;(2)f(x)为周期函数,且一个周期为4a。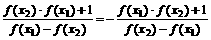
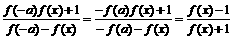
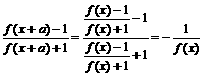
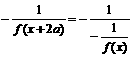 =f (x)
=f (x) 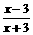
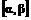 ,(β>α>0),判断f(x)在定义域上的增减性,并加以说明;
,(β>α>0),判断f(x)在定义域上的增减性,并加以说明;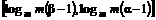 的定义域区间为
的定义域区间为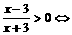 x<–3或x>3.
x<–3或x>3.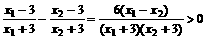
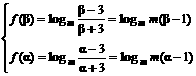
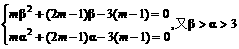
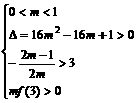 ∴0<m<
∴0<m<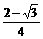
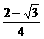 时,满足题意条件的m存在.
时,满足题意条件的m存在.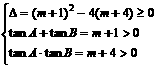 又A、B锐角为三角形内两内角
又A、B锐角为三角形内两内角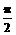 <A+B<π
<A+B<π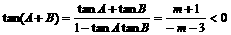
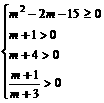 ∴m≥5
∴m≥5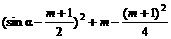
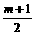 ≥2,∴当sinα=–1时,f(sinα)有最大值8.
≥2,∴当sinα=–1时,f(sinα)有最大值8.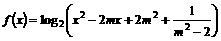 的定义域为实数集。(1)求实数m的所有允许值组成的集合M;(2)求证:对所有
的定义域为实数集。(1)求实数m的所有允许值组成的集合M;(2)求证:对所有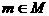 ,恒有
,恒有 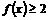 。
。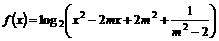 的定义域为实数集
的定义域为实数集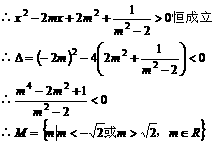
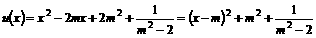
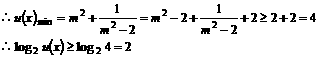
 =
=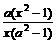 ,(a>0,a≠1),求证:(1)过函数y=f(x)图象上任意两点直线的斜率恒大于0;(2)f(3)>3。
,(a>0,a≠1),求证:(1)过函数y=f(x)图象上任意两点直线的斜率恒大于0;(2)f(3)>3。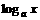 ,则x=
,则x=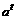 ,f(x)=
,f(x)= 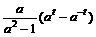 (t∈R)
(t∈R)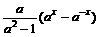 (x∈R)
(x∈R)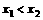 ,f(
,f(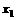 )-f(
)-f(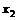 )=
)=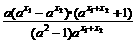
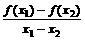 >0
>0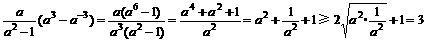
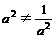 ∴上述不等式不能取等号,∴f(x)>3
∴上述不等式不能取等号,∴f(x)>3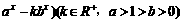 的定义域为(0,+∞),问是否存在这样的a,b,使f(x)恰在(1,+∞)上取正值,且f(3)=lg4,若存在,求出a,b的值,若不存在,说明理由。
的定义域为(0,+∞),问是否存在这样的a,b,使f(x)恰在(1,+∞)上取正值,且f(3)=lg4,若存在,求出a,b的值,若不存在,说明理由。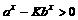 ,得
,得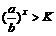 ,∵a>1>b>0,∴
,∵a>1>b>0,∴ >1,∴x>log
>1,∴x>log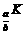
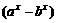
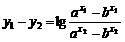 ,∵a>1>b>0,∴a
,∵a>1>b>0,∴a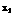 < a
< a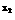 ,-b
,-b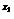 -b
-b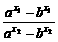 <1,∴lg
<1,∴lg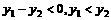 ,∴f(x)在(0,+∞)上是增函数
,∴f(x)在(0,+∞)上是增函数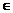 (1,+∞)时,必有f(x)>f(1)=lg(a-b)
(1,+∞)时,必有f(x)>f(1)=lg(a-b)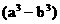 =lg4,
=lg4,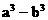 =4 (2)
=4 (2) 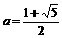 ,b=
,b=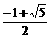 ,即有在
,即有在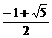 满足条件
满足条件 1, |f(-1)|
1, |f(-1)|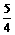
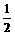 )2
)2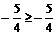 ∴[f(x)]
∴[f(x)]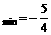
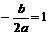 即b=-2a,∵a>0且b≠0 ∴b<0
即b=-2a,∵a>0且b≠0 ∴b<0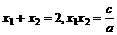 ,满足题设的充要条件是
,满足题设的充要条件是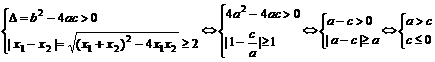
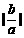
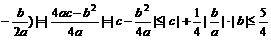
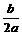 时取到,因|f(-1)|<1,
|f(1)|
时取到,因|f(-1)|<1,
|f(1)|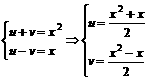
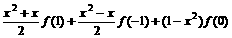
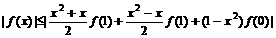 <
<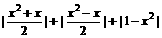 x∈[-1, 1]
x∈[-1, 1]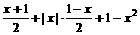 =
=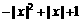 =
=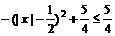
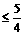
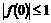 ,
,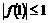 和
和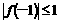 当成两个独立条件,先用
当成两个独立条件,先用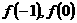 和
和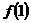 来表示
来表示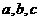 .
. 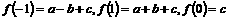 ,
,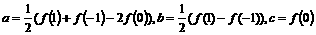 ,
,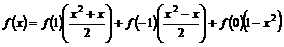 .
.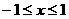 时,
时,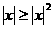 ,所以,根据绝对值不等式的性质可得:
,所以,根据绝对值不等式的性质可得: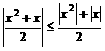 ,
,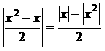 ,
,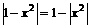
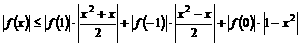
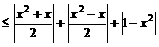
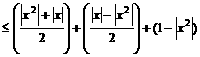
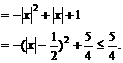
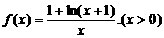
 )上是增函数还是减函数?证明你的结论;
)上是增函数还是减函数?证明你的结论;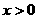 时,
时,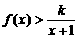 恒成立,求正整数
恒成立,求正整数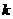 的最大值.
的最大值.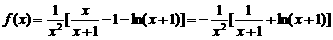
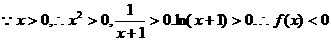 .
.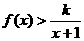 恒成立,令
恒成立,令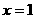 有
有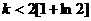
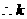 的最大值不大于3.……7′
的最大值不大于3.……7′
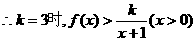 恒成立.
恒成立.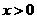 时,
时,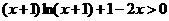 恒成立.
恒成立.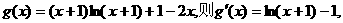

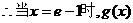 取得最小值
取得最小值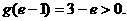
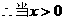 时,
时,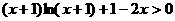 恒成立.
恒成立.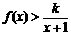 恒成立,
恒成立,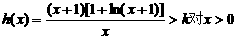 恒成立.
恒成立. 的最小值大于
的最小值大于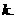
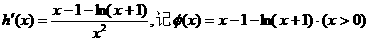
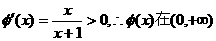 上连续递增,
上连续递增,
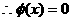 存在唯一实根
存在唯一实根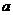 ,且满足:
,且满足: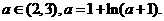
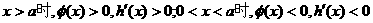 知:
知: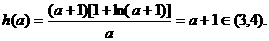
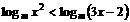 成立。
成立。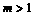 时,
时,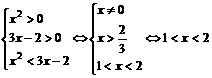
 时,
时,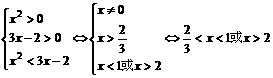
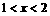
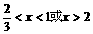 为所求。
为所求。