摘要：[例1] 设.则= 1 . 解:由=0.解得 [例2] 已知函数和定义在R上的奇函数.当x>0时..试求的反函数. 解: [例3] 已知函数是奇函数.又.求a.b.c的整数值. 解:由.又由.从而可得a=b=1,c=0 [例4] ⑴已知.求 ⑵在上的最小值为,试写出的解析式. 解:⑴. () ⑵ [例5] 已知函数.若的最大值为n.求的表达式. 解: [例6] 设是R上的偶函数.且在区间上递增.若成立.求a的取值范围. 解: 故为所求. [例7] 比较的大小. 解:作差比较大小: 当m > 1或0 < m < 1.都有u > 0 故. [例8] 设.(1)证明在上是增函数,(2)求及其 定义域 解:(1) 任取.且 是增函数. 在上是增函数 (2),定义域R.值域 反解: [例9] 定义在R上的函数满足:对任意实数.总有.且当时.． (1)试求的值, (2)判断的单调性并证明你的结论, (3)设.若.试确定的取值范围． (4)试举出一个满足条件的函数． 解:(1)在中.令．得: ． 因为.所以.． (2)要判断的单调性.可任取.且设． 在已知条件中.若取.则已知条件可化为:． 由于.所以． 为比较的大小.只需考虑的正负即可． 在中.令..则得． ∵ 时.. ∴ 当时.． 又.所以.综上.可知.对于任意.均有． ∴ ． ∴ 函数在R上单调递减． (3)首先利用的单调性.将有关函数值的不等式转化为不含的式子． . .即． 由.所以.直线与圆面无公共点．所以. ． 解得:． (4)如．
网址：http://m.1010jiajiao.com/timu3_id_523071[举报]
已知函数f(x)＝ax3＋bx2＋cx在x＝±1处取得极值，且在x＝0处的切线的斜率为－3.
(1)求f(x)的解析式；
(2)若过点A(2，m)可作曲线y＝f(x)的三条切线，求实数m的取值范围．
【解析】本试题主要考查了导数在研究函数中的运用。第一问，利用函数f(x)＝ax3＋bx2＋cx在x＝±1处取得极值，且在x＝0处的切线的斜率为－3，得到c＝－3 ∴a＝1, f(x)＝x3－3x
(2)中设切点为(x0，x03－3x0)，因为过点A(2，m)，所以∴m－(x03－3x0)＝(3x02－3)(2－x0)分离参数∴m＝－2x03＋6x02－6
然后利用g(x)＝－2x3＋6x2－6函数求导数，判定单调性，从而得到要是有三解，则需要满足－6<m<2
解：(1)f′(x)＝3ax2＋2bx＋c
依题意
又f′(0)＝－3
∴c＝－3 ∴a＝1 ∴f(x)＝x3－3x
(2)设切点为(x0，x03－3x0)，
∵f′(x)＝3x2－3，∴f′(x0)＝3x02－3
∴切线方程为y－(x03－3x0)＝(3x02－3)(x－x0)
又切线过点A(2，m)
∴m－(x03－3x0)＝(3x02－3)(2－x0)
∴m＝－2x03＋6x02－6
令g(x)＝－2x3＋6x2－6
则g′(x)＝－6x2＋12x＝－6x(x－2)
由g′(x)＝0得x＝0或x＝2
∴g(x)在(－∞，0)单调递减，(0,2)单调递增，(2，＋∞)单调递减．
∴g(x)极小值＝g(0)＝－6，g(x)极大值＝g(2)＝2
画出草图知，当－6<m<2时，m＝－2x3＋6x2－6有三解，
所以m的取值范围是(－6,2)．
查看习题详情和答案>>
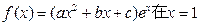处取得极小值，其图象过点A（0，1），且在点A处切线的斜率为—1。
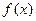的解析式；
上的值域也是
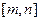，则称区间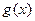
的“保值区间”。
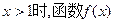不存在“保值区间”；