0 52257 52265 52271 52275 52281 52283 52287 52293 52295 52301 52307 52311 52313 52317 52323 52325 52331 52335 52337 52341 52343 52347 52349 52351 52352 52353 52355 52356 52357 52359 52361 52365 52367 52371 52373 52377 52383 52385 52391 52395 52397 52401 52407 52413 52415 52421 52425 52427 52433 52437 52443 52451 447348
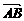 =a,
=a,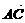 =b,a·b<0,S△ABC=
=b,a·b<0,S△ABC=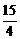 ,|a|=3,|b|=5,则a与b的夹角是( )
,|a|=3,|b|=5,则a与b的夹角是( )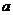 ,
,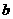 ,都有
,都有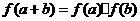 ”的函数例子.
”的函数例子.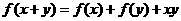 ,
,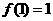 ,则f(25)= ___________________.
,则f(25)= ___________________.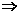
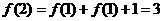
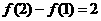
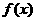 是定义在R上的偶函数,其图象关于直线
是定义在R上的偶函数,其图象关于直线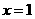 对称,对任意
对称,对任意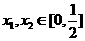 ,都有
,都有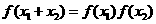
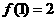 ,求
,求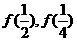
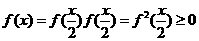 , x∈[0,1].
, x∈[0,1].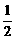 )·f(
)·f(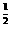 .
.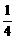 )·f(
)·f(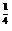 .
.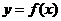 关于直线x=1对称,故f(x)=f(1+1-x)
关于直线x=1对称,故f(x)=f(1+1-x) f(x)=f(2-x),x∈R.
f(x)=f(2-x),x∈R.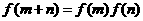 且当
且当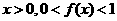
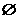 ,求a的取值范围.
,求a的取值范围.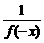 >1.
>1.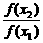 <1.∴f(x2)<f(x1).
<1.∴f(x2)<f(x1).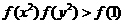
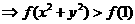
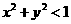
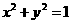 相离或相切。
相离或相切。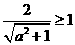
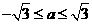
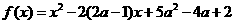 在区间[0,1]上的最小值
在区间[0,1]上的最小值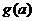 的表达式.
的表达式.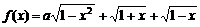 的最大值为g(a).
的最大值为g(a).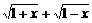 ,求t的取值范围,并把f(x)表示为t的函数m(t)
,求t的取值范围,并把f(x)表示为t的函数m(t)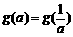 的所有实数a
的所有实数a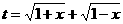 ,
,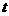 有意义,必须
有意义,必须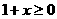 且
且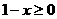 ,即
,即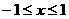
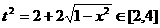 ,且
,且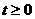 ……① ∴
……① ∴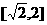 。
。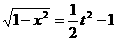 ,∴
,∴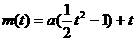
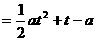 ,
,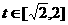 。
。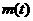
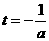 是抛物线
是抛物线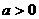 时,函数
时,函数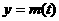 ,
,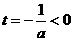 知
知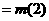
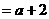 ;
;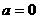 时,
时,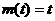 ,
,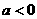 时,,函数
时,,函数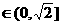 即
即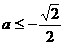 时,
时,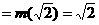 ,
,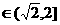 即
即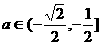 时,
时,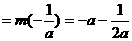 ,
,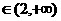 即
即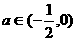 时,
时,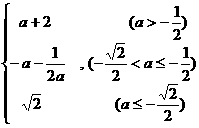 。
。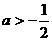 时,
时,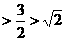 ;
;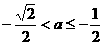 时,
时,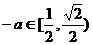 ,
,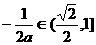 ,∴
,∴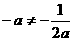 ,
,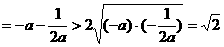 ,故当
,故当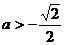 时,
时,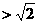 ;
;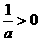 ,由
,由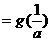 知:
知: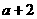
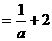 ,故
,故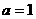 ;
;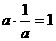 ,故
,故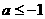 或
或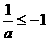 ,从而有
,从而有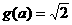 或
或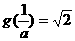 ,
,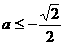 ,
,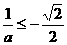 ,即
,即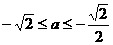 ,
,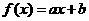 ,则
,则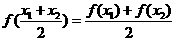
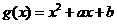 ,则
,则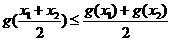
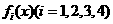 是定义在[0,1]上的四个函数,其中满足性质:“对[0,1]中任意的
是定义在[0,1]上的四个函数,其中满足性质:“对[0,1]中任意的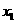 和
和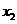 ,任意
,任意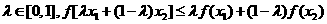 恒成立”的只有 ( )
恒成立”的只有 ( )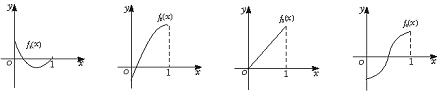
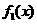
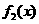
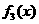
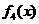
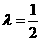 时,符合条件的函数是凹函数,从图像可看出有
时,符合条件的函数是凹函数,从图像可看出有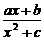 的图象如下图所示,则a、b、c的大小关系是
的图象如下图所示,则a、b、c的大小关系是 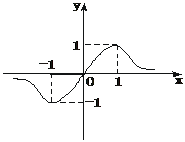
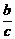 =0,∴b=0.f(1)=1,∴
=0,∴b=0.f(1)=1,∴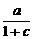 =1.
=1.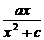 >0,
>0,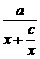 ,
,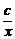 ≥2
≥2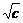 ,
,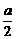 =1.∴a=2.
=1.∴a=2.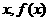 表示弧AB与弦AB
表示弧AB与弦AB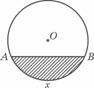 所围成的弓形面积的2倍,则函数
所围成的弓形面积的2倍,则函数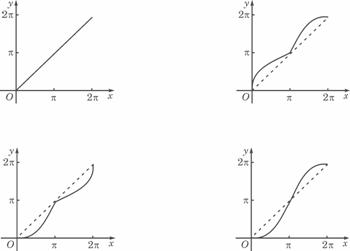
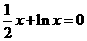 (2)
(2)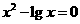
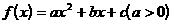 ,方程
,方程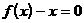 的两个根
的两个根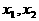 满足
满足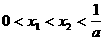 . 当
. 当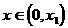 时,证明
时,证明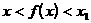 .
.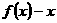 的表达式,从而得到函数
的表达式,从而得到函数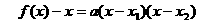 .
.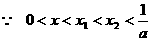 ,
,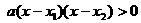 ,
,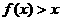 .
.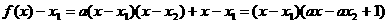 ,
,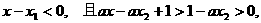
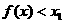 ,
,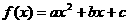 .
.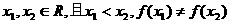 ,方程
,方程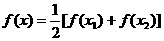 有2个不等实根,
有2个不等实根,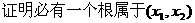
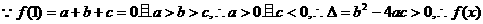
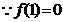 ,∴1是
,∴1是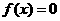 的一个根,由韦达定理知另一根为
的一个根,由韦达定理知另一根为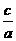 ,
,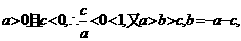
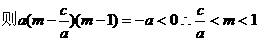
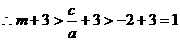
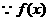 在(1,+∞)单调递增,
在(1,+∞)单调递增,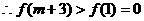 ,即存在这样的m使
,即存在这样的m使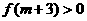
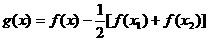 ,则
,则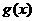 是二次函数.
是二次函数.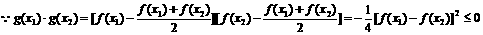
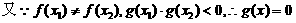 有两个不等实根,且方程
有两个不等实根,且方程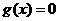 的根必有一个属于
的根必有一个属于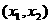 .
.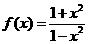 ,求证:(1)
,求证:(1)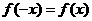 (2)
(2)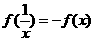
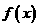 对于任意实数
对于任意实数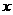 满足条件
满足条件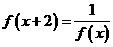 ,若
,若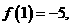 则
则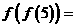 __________.
__________.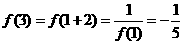 ,
,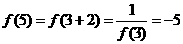 ,又
,又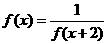 ,
,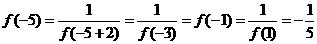
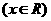 满足
满足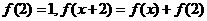 ,则
,则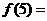
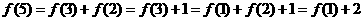 ,令
,令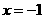 ,则
,则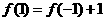 ,又∵
,又∵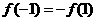 ,
,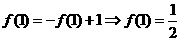 ,∴
,∴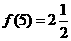
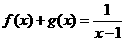 ,则
,则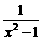 B.
B.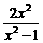 C.
C.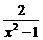 D.
D.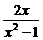
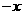 代
代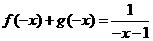 ,即
,即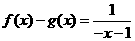 ②
②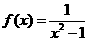
 ,
,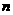 的大小
的大小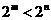 (2)
(2)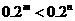
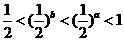 ,那么 ( )
,那么 ( )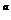 <a
<a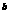 <b
<b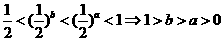 ,在A和B中,
,在A和B中,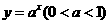 在定义域内是单调递减的,∴
在定义域内是单调递减的,∴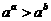 ,所以结论不成立.在C中,
,所以结论不成立.在C中,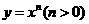 在
在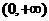 内是单调递增的,又
内是单调递增的,又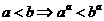 ,所以答案为C.
,所以答案为C.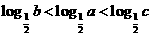 ,则 ( )
,则 ( )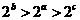 B.
B.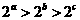
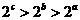 D.
D.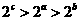
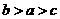 ,因为
,因为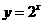 在定义域内是单调递增的,所以
在定义域内是单调递增的,所以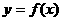 的图象与函数
的图象与函数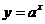 (
(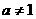 )的图象关于直线
)的图象关于直线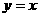 对称,记
对称,记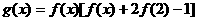 .若
.若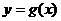 在区间
在区间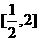 上是增函数,则实数
上是增函数,则实数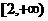 B.
B. C.
C.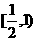 D.
D.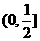
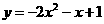 ,
,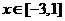
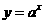 在[0,1]上的最大值与最小值的和为3,则
在[0,1]上的最大值与最小值的和为3,则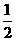 B.2 C.4
D.
B.2 C.4
D.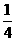
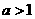 或
或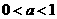 时,函数
时,函数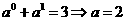 ,故选C.
,故选C. 在区间
在区间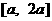 上的最大值是最小值的3倍,则
上的最大值是最小值的3倍,则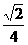 B.
B.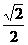 C.
C.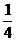 D.
D.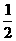
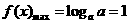 ,
,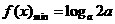 ,∴
,∴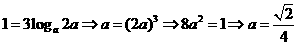 ,故选A
,故选A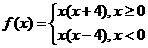 ,求
,求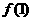 ,
,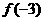 ,
,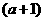 的值
的值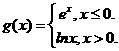 则
则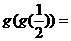 __________
__________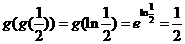 .
.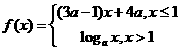 是
是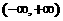 上的减函数,那么
上的减函数,那么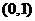 B.
B.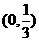
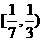 D.
D.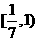
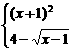
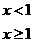 则使得f(x)≥1的自变量x的取值范围为
则使得f(x)≥1的自变量x的取值范围为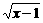 ≥1
≥1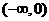 上是增函数还是减函数,并证明你的判断.
上是增函数还是减函数,并证明你的判断.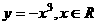 B.
B.
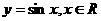
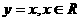 D.
D.
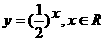
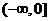 上是增函数,若
上是增函数,若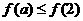 ,则实数
,则实数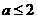 B.
B.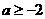 C.
C.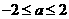 D.
D.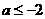 或
或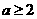
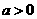 时,∵函数
时,∵函数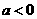 时,函数
时,函数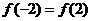 ,∴
,∴