0 52263 52271 52277 52281 52287 52289 52293 52299 52301 52307 52313 52317 52319 52323 52329 52331 52337 52341 52343 52347 52349 52353 52355 52357 52358 52359 52361 52362 52363 52365 52367 52371 52373 52377 52379 52383 52389 52391 52397 52401 52403 52407 52413 52419 52421 52427 52431 52433 52439 52443 52449 52457 447348
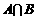 B.
B.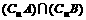 C.
C. 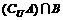 D.
D.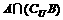
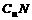 ) B.MÊ(
) B.MÊ(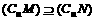 D.
D.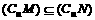
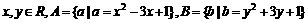 ,求集合A与B之间的关系。
,求集合A与B之间的关系。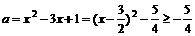 ,得A=
,得A=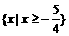
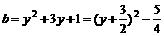
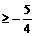
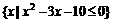 ,集合B=
,集合B=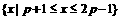 ,若B
,若B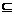 A,求实数p
A,求实数p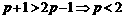
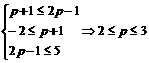
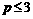 时,B
时,B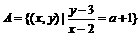 ,集合B=
,集合B=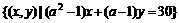 。如果
。如果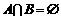 ,
,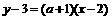 ,
,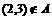 ,只有
,只有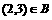 才满足条件。
才满足条件。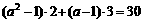 ;解得:a=-5或a=
;解得:a=-5或a=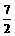
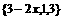 ,B=
,B=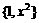 ,且
,且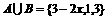 ,求实数x。
,求实数x。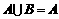 ,∴
,∴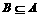 ,故
,故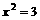 或
或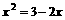
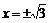 或
或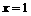 或
或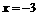 ,但当
,但当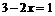 不满足集合A的条件。
不满足集合A的条件。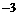 或
或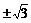 。
。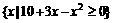 ,B=
,B=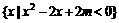 ,若
,若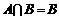 ,求实数m的值。
,求实数m的值。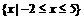 ,由
,由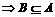 ,又
,又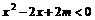 ,
,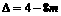
 ,即
,即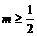 ,则
,则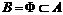
 ,即
,即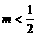 ,
,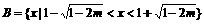 ,
,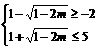
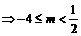
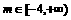
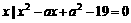 },B=
},B=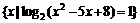 ,C=
,C=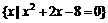 ,
,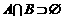 与
与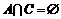 同时成立,求实数a的值。
同时成立,求实数a的值。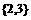 ,C=
,C=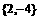 ,由
,由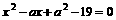
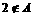 ,即
,即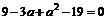 得,a=5或a=-2
得,a=5或a=-2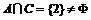 ,故a=5舍去。
,故a=5舍去。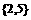 ,于是
,于是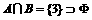 ,∴a=-2。
,∴a=-2。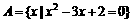 ,
,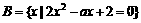 ,A∪B=A,求a的取值构成的集合。
,A∪B=A,求a的取值构成的集合。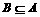 ,当
,当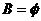 时
时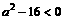 ,∴-4<a<4,
,∴-4<a<4,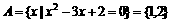 ,当1∈B时,将x=1代入B中方程得a=4,此时B={1},当2∈B时,将x=2代入B中方程得a=5,此时
,当1∈B时,将x=1代入B中方程得a=4,此时B={1},当2∈B时,将x=2代入B中方程得a=5,此时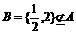 ,a=5舍去,∴-4<a≤4。
,a=5舍去,∴-4<a≤4。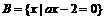 且A∪B=A,求实数a组成的集合C。
且A∪B=A,求实数a组成的集合C。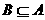 ,只需a×1-2=0,a=2或a×2-2=0,a=1。
,只需a×1-2=0,a=2或a×2-2=0,a=1。 (1)只乘电车的人数;(2)不乘电车的人数;(3)乘车的人数;
(1)只乘电车的人数;(2)不乘电车的人数;(3)乘车的人数;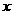 的不等式
的不等式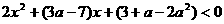 的解集,且M中的一个元素是0,求实数
的解集,且M中的一个元素是0,求实数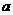 的取值范围,并用
的取值范围,并用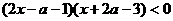 ,
,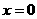 适合不等式故得
适合不等式故得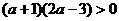 ,所以
,所以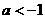 ,或
,或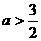 .
.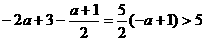 ,∴
,∴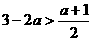 ,
,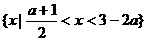 ;
;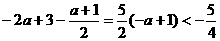 ,∴
,∴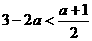 ,
,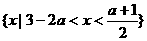 .
.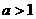 ,设命题
,设命题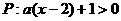 ,命题
,命题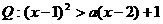 .试寻求使得
.试寻求使得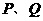 都是真命题的
都是真命题的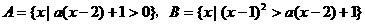 ,
,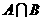 ,
,
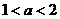 时,则有
时,则有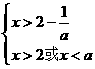 ,
,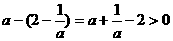 ,所以
,所以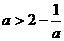 ,
即当
,
即当 ;
;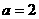 时易得使
时易得使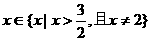 ;
;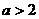 ,则有
,则有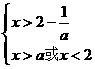 ,
,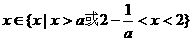 .
.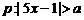 和条件
和条件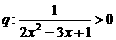 ,请选取适当的实数
,请选取适当的实数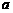 的值,分别利用所给的两个条件作为A、B构造命题:“若A则B”,并使得构造的原命题为真命题,而其逆命题为假命题.则这样的一个原命题可以是什么?并说明为什么这一命题是符合要求的命题.
的值,分别利用所给的两个条件作为A、B构造命题:“若A则B”,并使得构造的原命题为真命题,而其逆命题为假命题.则这样的一个原命题可以是什么?并说明为什么这一命题是符合要求的命题.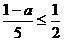 ,且
,且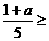 1即可.这种新颖的命题形式有较强的综合性,同时也是对于四个命题考查的一种新尝试,如此命题可以考查学生探究问题、解决问题的能力,符合当今倡导研究性学习的教学方向.
1即可.这种新颖的命题形式有较强的综合性,同时也是对于四个命题考查的一种新尝试,如此命题可以考查学生探究问题、解决问题的能力,符合当今倡导研究性学习的教学方向.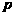 即
即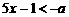 ,或
,或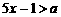 ,∴
,∴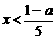 ,或
,或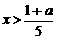 ,
,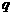 即
即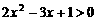 ,∴
,∴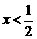 ,或
,或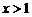 ;
;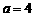 ,则
,则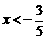 ,或
,或 成立,反之不然.
成立,反之不然.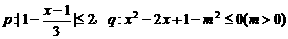 ;¬
;¬ 的取值范围.
的取值范围.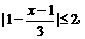 得
得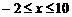 ,
,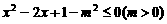 ,得
,得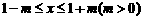 ,
,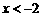 ,或
,或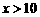 ,而¬
,而¬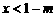 ,或
,或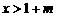
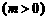 ;
;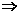 ¬
¬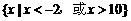 ,B=
,B=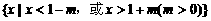 ,
,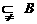 ,故
,故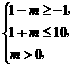 且不等式中的第一、二两个不等式不能同时取等号,
且不等式中的第一、二两个不等式不能同时取等号,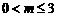 ,此即为“¬
,此即为“¬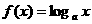 ,其中
,其中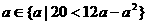 .
.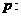
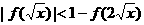 为真命题,求实数
为真命题,求实数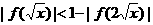 为真命题,求实数
为真命题,求实数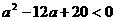 ,
,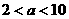 ,∴函数
,∴函数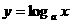 是增函数;
是增函数;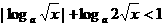 ,必有
,必有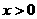 ,
,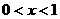 ,
,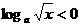 ,不等式化为
,不等式化为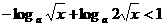 ,
,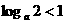 ,这显然成立,此时
,这显然成立,此时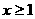 时,
时,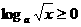 ,不等式化为
,不等式化为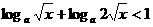 ,
,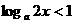 ,故
,故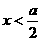 ,此时
,此时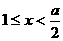 ;
;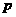 为真命题的
为真命题的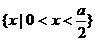 .
.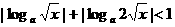 ,必有
,必有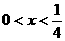 时,
时,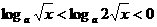 ,不等式化为
,不等式化为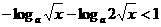 ,
,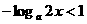 ,故
,故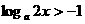 ,∴
,∴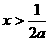 ,此时
,此时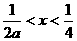 ;
;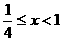 时,
时,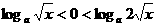 ,不等式化为
,不等式化为 ,不等式化为
,不等式化为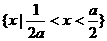 .
.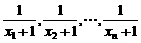 为等差数列.
为等差数列.