5.坐标变换
坐标变换 在解析几何中,把坐标系的变换(如改变坐标系原点的位置或坐标轴的方向)叫做 坐标变换.实施坐标变换时,点的位置,曲线的形状、大小、位置都不改变,仅仅只改变点 的坐标与曲线的方程.
坐标轴的平移 坐标轴的方向和长度单位不改变,只改变原点的位置,这种坐标系的变换叫 做坐标轴的平移,简称移轴.
坐标轴的平移公式 设平面内任意一点M,它在原坐标系xOy中的坐标是9x,y),在新坐标系x ′O′y′中的坐标是(x′,y′).设新坐标系的原点O′在原坐标系xOy中的坐标是(h,k),则
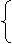
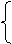 x=x′+h
x′=x-h
x=x′+h
x′=x-h
(1) 或(2)
y=y′+k y′=y-k
公式(1)或(2)叫做平移(或移轴)公式.
中心或顶点在(h,k)的圆锥曲线方程
中心或顶点在(h,k)的圆锥曲线方程见下表.
|
方 程 |
焦 点 |
焦 线 |
对称轴 |
|
|
椭圆 |
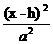 + +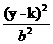 =1 =1 |
(±c+h,k) |
x=±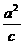 +h +h |
x=h y=k |
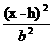 + +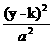 =1 =1 |
(h,±c+k) |
y=±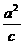 +k +k |
x=h y=k |
|
|
双曲线 |
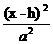 - -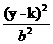 =1 =1 |
(±c+h,k) |
=±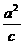 +k +k |
x=h y=k |
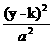 - -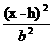 =1 =1 |
(h,±c+h) |
y=±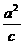 +k +k |
x=h y=k |
|
|
抛物线 |
(y-k)2=2p(x-h) |
(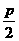 +h,k) +h,k) |
x=-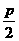 +h +h |
y=k |
|
(y-k)2=-2p(x-h) |
(-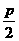 +h,k) +h,k) |
x=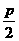 +h +h |
y=k |
|
|
(x-h)2=2p(y-k) |
(h, 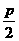 +k) +k) |
y=-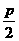 +k +k |
x=h |
|
|
(x-h)2=-2p(y-k) |
(h,- 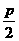 +k) +k) |
y=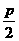 +k +k |
x=h |
3.椭圆、双曲线和抛物线
椭圆、双曲线和抛物线的基本知识见下表.
 |
椭 圆 |
双曲线 |
抛物线 |
|||
|
轨迹条件 |
点集:({M||MF1+|MF2|=2a,|F 1F2|<2a= |
点集:{M||MF1|-|MF2|. =±2a,|F2F2|>2a}. |
点集{M| |MF|=点M到直线l的距离}. |
|||
|
圆 形 |
|
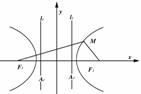 |
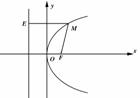 |
|||
|
标准方程 |
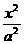 + +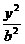 =1(a>b>0) =1(a>b>0) |
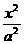 - -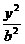 =1(a>0,b>0) =1(a>0,b>0) |
y2=2px(p>0) |
|||
|
顶 点 |
A1(-a,0),A2(a,0); B1(0,-b),B2(0,b) |
A1(0,-a),A2(0,a) |
O(0,0) |
|||
|
轴 |
对称轴x=0,y=0 长轴长:2a 短轴长:2b |
对称轴x=0,y=0 实轴长:2a 虚轴长:2b |
对称轴y= |
|||
|
焦 点 |
F1(-c,0),F2(c,0) 焦点在长轴上 |
F1(-c,0),F2(c,0) 焦点在实轴上 |
F(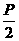 ,0) ,0)焦点对称轴上 |
|||
|
焦 距 |
|F1F2|=2c, c= 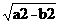 |
|F1F2|=2c, c= 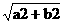 |
|
|||
|
准 线 |
x=±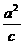 准线垂直于长轴,且在椭圆外. |
x=±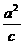 准线垂直于实轴,且在两顶点的内侧. |
x=-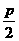 准线与焦点位于顶点两侧,且到顶点的距离相等. |
|||
|
离心率 |
e=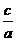 ,0<e<1 ,0<e<1 |
e=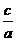 ,e>1 ,e>1 |
e=1 |
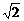 )的椭圆被直线3x-y-2=0截得的弦的中点的横坐标为
)的椭圆被直线3x-y-2=0截得的弦的中点的横坐标为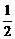 ,则椭圆方程为( )
,则椭圆方程为( )
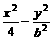 =1(b∈N)的两个焦点F1、F2,P为双曲线上一点,
=1(b∈N)的两个焦点F1、F2,P为双曲线上一点,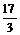 ,
,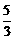 ,∴b2=1.
,∴b2=1.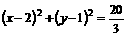 ,椭圆C2的方程为
,椭圆C2的方程为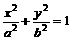
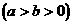 ,C2的离心率为
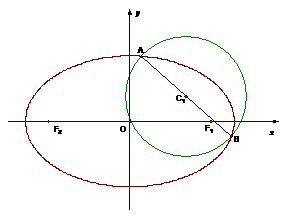
,C2的离心率为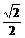 ,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,求直线AB的方程和椭圆C2的方程。
,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,求直线AB的方程和椭圆C2的方程。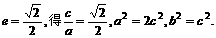
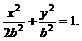
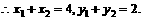
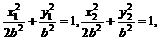
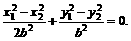
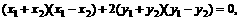
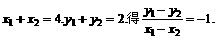
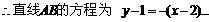
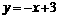
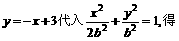
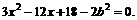

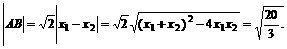
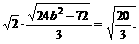
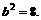 故所有椭圆方程
故所有椭圆方程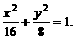
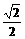 的椭圆C相交于A、B两点,直线y=
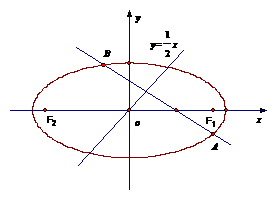
的椭圆C相交于A、B两点,直线y=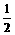 x过线段AB的中点,同时椭圆C上存在一点与右焦点关于直线l对称,试求直线l与椭圆C的方程.
x过线段AB的中点,同时椭圆C上存在一点与右焦点关于直线l对称,试求直线l与椭圆C的方程.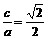 ,得
,得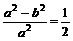 ,从而a2=2b2,c=b.
,从而a2=2b2,c=b.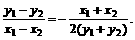
 设AB中点为(x0,y0),则kAB=-
设AB中点为(x0,y0),则kAB=-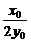 ,
,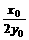 =-1,kAB=-1,
=-1,kAB=-1,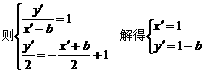
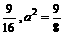 .
.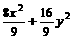 =1,l的方程为y=-x+1.
=1,l的方程为y=-x+1.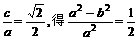 ,从而a2=2b2,c=b.
,从而a2=2b2,c=b.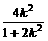 ,y1+y2=k(x1-1)+k(x2-1)=k(x1+x2)-2k=-
,y1+y2=k(x1-1)+k(x2-1)=k(x1+x2)-2k=-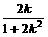 .
.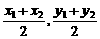 ),则
),则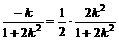 ,
,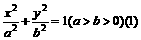
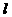 不平行于y轴,否则AB中点在x轴上与直线
不平行于y轴,否则AB中点在x轴上与直线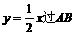 中点矛盾。
中点矛盾。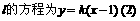

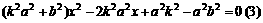
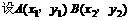 ,
,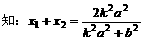
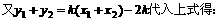
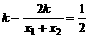 ,
,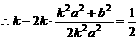 ,
,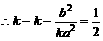 ,
,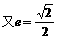
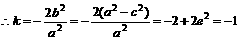 ,
,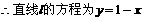 ,
,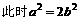 ,
,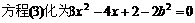 ,
,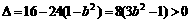
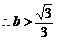 ,
,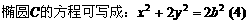 ,
,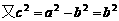 ,
,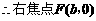 ,
,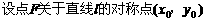 ,
,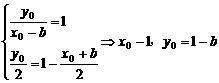 ,
,
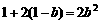 ,
,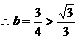 ,
,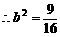 ,
, 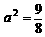
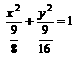
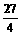 ,P为线段P1P2的一个三等分点,求以直线OP1、OP2为渐近线且过点P的离心率为
,P为线段P1P2的一个三等分点,求以直线OP1、OP2为渐近线且过点P的离心率为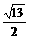 的双曲线方程.
的双曲线方程.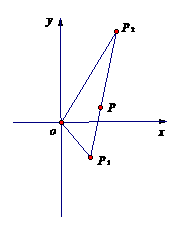 解:以O为原点,∠P1OP2的角平分线为x轴建立如图所示的直角坐标系.
解:以O为原点,∠P1OP2的角平分线为x轴建立如图所示的直角坐标系.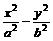 =1(a>0,b>0)
=1(a>0,b>0)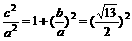 ,得
,得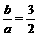 .
.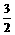 x和y=-
x和y=-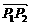 所成的比λ=
所成的比λ=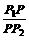 =2,
=2,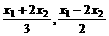 ),
),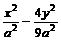 =1上,
=1上,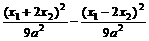 =1,
=1,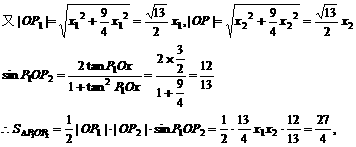
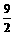 ②
②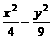 =1.
=1.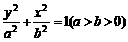 上一动点P引圆O:x2 +y2 =b2的两条切线PA、PB,A、B为切点,直线AB与x轴,y轴分别交于M、N两点。(1) 已知P点坐标为(x0,y0 )并且x0y0≠0,试求直线AB方程;(2) 若椭圆的短轴长为8,并且
上一动点P引圆O:x2 +y2 =b2的两条切线PA、PB,A、B为切点,直线AB与x轴,y轴分别交于M、N两点。(1) 已知P点坐标为(x0,y0 )并且x0y0≠0,试求直线AB方程;(2) 若椭圆的短轴长为8,并且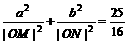 ,求椭圆C的方程;(3) 椭圆C上是否存在点P,由P向圆O所引两条切线互相垂直?若存在,
,求椭圆C的方程;(3) 椭圆C上是否存在点P,由P向圆O所引两条切线互相垂直?若存在,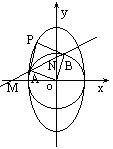 请求出存在的条件;若不存在,请说明理由。
请求出存在的条件;若不存在,请说明理由。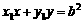 ,PB:
,PB: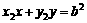
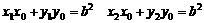
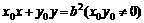
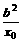 ,0);令x=0,则N(0,
,0);令x=0,则N(0,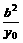 )
)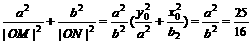 ①
①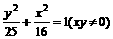 (注:不剔除xy≠0,可不扣分)
(注:不剔除xy≠0,可不扣分)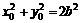 ①
① 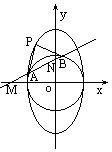
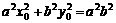 ②
②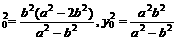
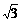 ,0)、F2(
,0)、F2(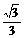 ,过F2点且倾斜角为锐角的直线l与椭圆C交于A、B两点,使得|F2B|=3|F2A|.
,过F2点且倾斜角为锐角的直线l与椭圆C交于A、B两点,使得|F2B|=3|F2A|.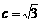
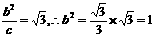 ,
, a2=b2+c2=1+3=4
a2=b2+c2=1+3=4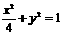
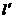 与l交于点P,作AM⊥
与l交于点P,作AM⊥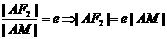
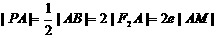 …9分
…9分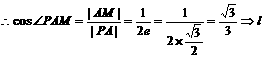 的斜率
的斜率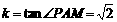 .
.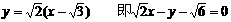
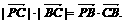
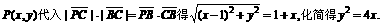
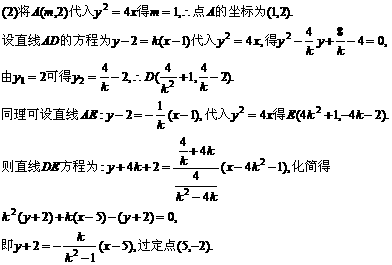

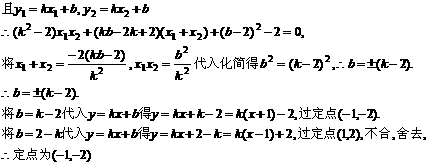
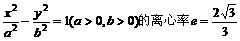 ,直线l过A(a,0)、
,直线l过A(a,0)、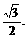
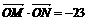 ,求直线m的方程.
,求直线m的方程.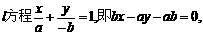 由原点O到l的距离
由原点O到l的距离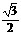 ,得
,得 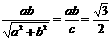 又
又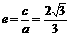
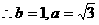
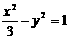
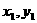 )、
)、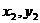 )是方程组
)是方程组 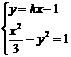 的解
的解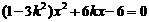 ①
①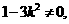 由根与系数关系,知
由根与系数关系,知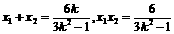
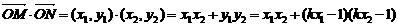
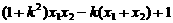 =
=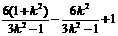
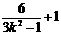
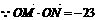 ∴
∴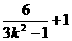 =-23,k=±
=-23,k=±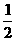
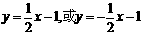
 与双曲线
与双曲线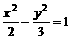 的两个焦点
的两个焦点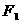 、
、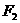 的距离之和为定值,且
的距离之和为定值,且
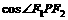 的最小值为
的最小值为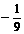 .
.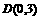 ,
,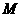 、
、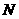 在动点
在动点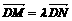 ,求实数
,求实数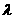 的取值范围.
的取值范围.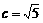 ,
,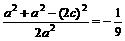
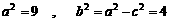
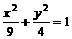 .
. 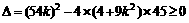 ,得
,得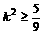 .
. 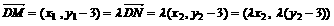 ,得
,得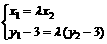
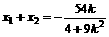 ,
,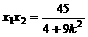 ②
② 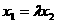 代入②式并消去 x 2可得
代入②式并消去 x 2可得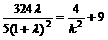 ,由前面知,
,由前面知,
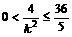
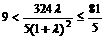 ,解得
,解得 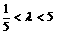 .
. 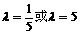 ,
,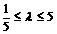 为所求。
为所求。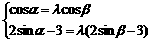
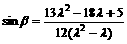 , 由于
, 由于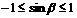
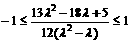 , 解得
, 解得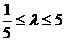 为所求.
为所求. 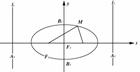
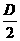 ,-
,-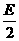 ,半径是
,半径是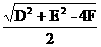 .配方,将方程x2+y2+Dx+Ey+F=0化为
.配方,将方程x2+y2+Dx+Ey+F=0化为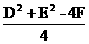
 点M在圆C内,
点M在圆C内,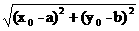 .
.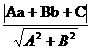 与半径r的大小关系来判定.
与半径r的大小关系来判定. f1(x0,y0)=0
f1(x0,y0)=0