0 52203 52211 52217 52221 52227 52229 52233 52239 52241 52247 52253 52257 52259 52263 52269 52271 52277 52281 52283 52287 52289 52293 52295 52297 52298 52299 52301 52302 52303 52305 52307 52311 52313 52317 52319 52323 52329 52331 52337 52341 52343 52347 52353 52359 52361 52367 52371 52373 52379 52383 52389 52397 447348
 是
是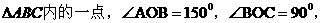
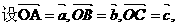 且
且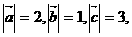 试用
试用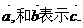
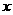 轴和
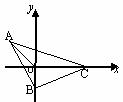
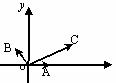
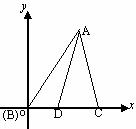
轴和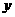 轴建立如图3所示的坐标系.
轴建立如图3所示的坐标系.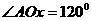 ,所以
,所以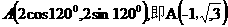 ,
, 易求
易求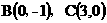 ,设
,设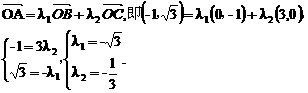
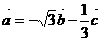 .
.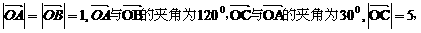
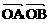 表示
表示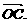
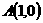 ,
,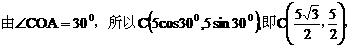

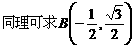
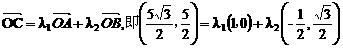
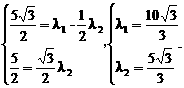
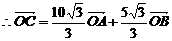 .
.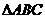 ,AD为中线,求证
,AD为中线,求证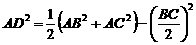
 设
设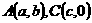 ,
,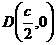 ,
,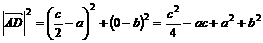 ,
,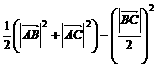 .
.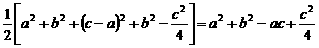 ,
,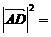
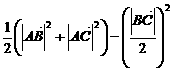 ,
,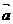 =(x1,y1)、
=(x1,y1)、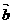 =(x2,y2),则
=(x2,y2),则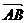 |=
|=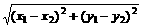
 x1x2+y1y2=0
x1x2+y1y2=0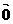 或
或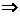 x1x2+y1y2=0、但反过来,当x1x2+y1y2=0时,可以是x1=y1=0,即
x1x2+y1y2=0、但反过来,当x1x2+y1y2=0时,可以是x1=y1=0,即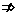
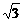 ,-1),
,-1), 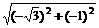 =2
=2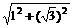 =2
=2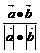 =
=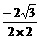 =
=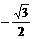
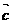 使得:
使得: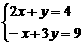
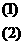
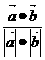 =
=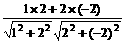 =-
=-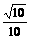
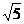 ×(-
×(-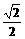
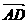 及点D的坐标、
及点D的坐标、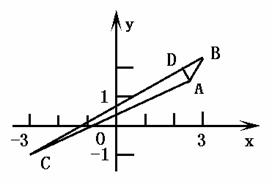 ∴AD⊥BC,∴
∴AD⊥BC,∴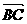
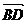
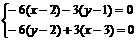
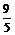 ,y=
,y=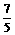
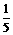 ,
,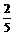 )
)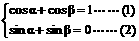
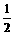
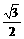 ,sinβ=
,sinβ=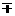
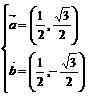 或
或
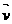 =(x,y)|x2+y2≤1}中的任意两个向量
=(x,y)|x2+y2≤1}中的任意两个向量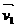 、
、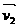 与两个非负实数α、β;求证:向量α
与两个非负实数α、β;求证:向量α
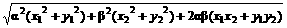
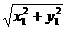
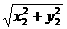 ≤1
≤1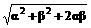 =|α+β|=α+β
=|α+β|=α+β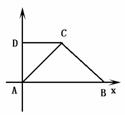 则A(0,0)、B(2,0)、C(1,1)、D(0,1)
则A(0,0)、B(2,0)、C(1,1)、D(0,1)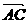 =(1,1)
=(1,1)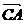 =(-x,a),
=(-x,a), 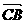 =(-x,b)
=(-x,b)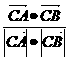 =
=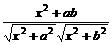
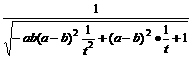
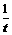 =
=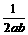 即t=2ab时,cos∠ACB最大值为
即t=2ab时,cos∠ACB最大值为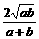 、
、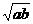 ,0)时,∠ACB最大值为arccos
,0)时,∠ACB最大值为arccos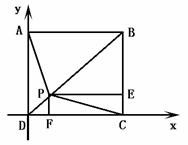 如图,四边形ABCD是正方形,P是对角线BD上的一点,PECF是矩形,用向量法证明
如图,四边形ABCD是正方形,P是对角线BD上的一点,PECF是矩形,用向量法证明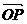 |=λ,则A(0,1),P(
|=λ,则A(0,1),P(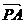 =(-
=(-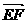 =(
=(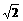 λ+1
λ+1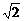 λ+1
λ+1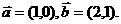
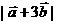 ;
; 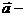
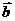 与
与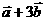 平行, 平行时它们是同向还是反向?
平行, 平行时它们是同向还是反向?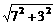 =
=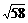 .
.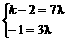
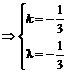 .
. 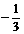 时, 它们反向平行.
时, 它们反向平行.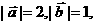
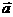 与
与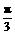 ,若向量
,若向量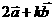 与
与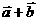 垂直, 求k.
垂直, 求k.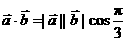 =2×1×
=2×1×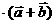 =
= 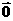 ,
, 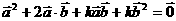
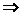 k = - 5.
k = - 5.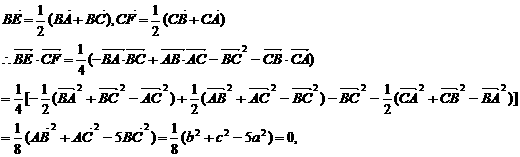
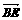 ⊥
⊥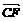 , 即 BE⊥CF .
, 即 BE⊥CF .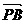 ,
,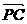 ,
,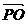 两两不共线,有
两两不共线,有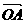 +
+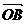 )·(
)·(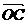 +
+ =(2
=(2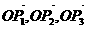 满足条件
满足条件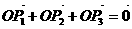 ,
,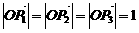 ,求证:
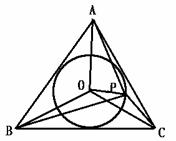
,求证: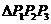 是正三角形
是正三角形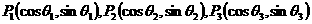
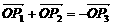 ,即
,即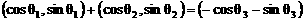
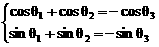
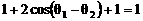 ,
,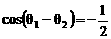 ,
,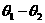 的最小正角为
的最小正角为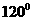 ,即
,即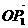 与
与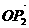 的夹角为
的夹角为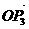 的夹角为
的夹角为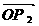 与
与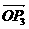 的夹角为
的夹角为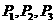 三点均匀分部在一个单位圆上,
三点均匀分部在一个单位圆上,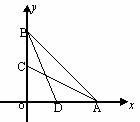 解:如图,分别以等腰直角三角形的两直角边为
解:如图,分别以等腰直角三角形的两直角边为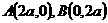 ,则
,则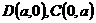 ,
,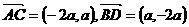 ,
,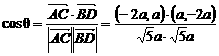 =
=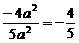 .
.  .
.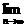 S2n<3,求q的取值范围.
S2n<3,求q的取值范围.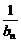 )(其中a>0且a≠1)记Sn是数列{an}的前n项和,试比较Sn与
)(其中a>0且a≠1)记Sn是数列{an}的前n项和,试比较Sn与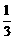 logabn+1的大小,并证明你的结论.
logabn+1的大小,并证明你的结论.