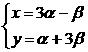7、极坐标方程ρcosθ=sin2θ表示的曲线是
A、一个圆 B、一条直线和一条射线
C、一条直线及一个圆 D、一条射线及一个圆
|
8、直线 |
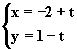 |
(t为参数)被曲线 |
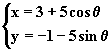 |
(θ为参数)所截得的弦长为 |
|
A、 |
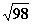 |
B、161/4 C、 |
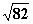 |
D、 |
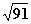 |
|
9、(x、y)是曲线 |
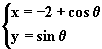 |
(θ为参数,0≤θ<π)上的点;则y/x的取值范围是 |
|
A、 |
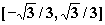 |
B、 |
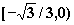 |
|
C、 |
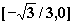 |
D、 |
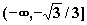 |
|
||
|
10、在极坐标中,极点到直线 |
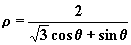 |
的距离为 。 |
||||
|
11、双曲线 |
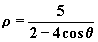 |
焦距为 。 |
|
||
|
12、曲线 |
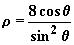 |
的直角坐标方程为 。 |
|||
|
13、直线 |
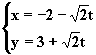 |
(t为参数)上与点(-2,3)的距离等于 |
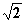 |
的点的坐标为 |
|
14、极坐标方程 |
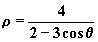 |
表示的曲线中,离极点较近的那条准线的极坐标方程为
。 |
|
15、已知一个圆的极坐标方程为 |
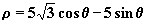 |
,则圆心的极坐标为 。 |
2、已知点A(-4,7π/6)和点B关于直线θ=π/3(ρ∈R)对称,求点B的坐标
A、(-4,π/2) B、(-4,3π/ 2)
C、(4,π) D、(4,3π/2)
|
3、直线 |
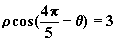 |
与直线 |
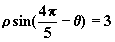 |
的位置关系是 |
A、平行 B、相交但不垂直
C、垂直 D、重合
|
4、方程 |
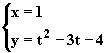 |
(t为参数)表示的图形是 |
A、直线 B、一条射线
C、抛物线 D、两条射线
|
5、极坐标方程 |
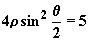 |
表示的曲线是 |
A、圆 B、椭圆
C、双曲线的一支 D、抛物线
|
6、参数方程 |
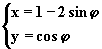 |
(ψ为参数)所表示的曲线是 |
A、焦点在x轴上的双曲线 B、焦点在y轴上的双曲线
C、焦点在x轴上的椭圆 D、焦点在y轴上的椭圆
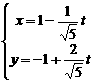 (t为参数)的斜率和倾斜角分别是( )
(t为参数)的斜率和倾斜角分别是( )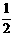 和arctg(-
和arctg(-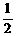 )
) 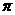 -arctg2 D) -
-arctg2 D) -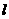 的方程:
的方程: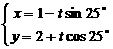 (t为参数),那么直线
(t为参数),那么直线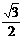 的直线
的直线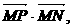
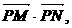
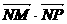 成公差小于零的等差数列.
成公差小于零的等差数列.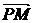 与
与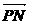 的夹角,求tanθ.
的夹角,求tanθ.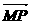 =(-1-x,-y),
=(-1-x,-y),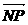 =(1-x,-y),
=(1-x,-y),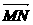 =-
=-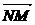 =(2,0)
=(2,0)
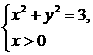
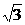 为半径的右半圆.
为半径的右半圆.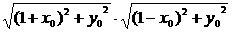 .
.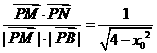
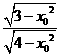
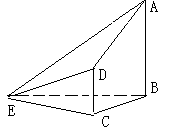
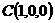 ,
,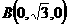 ,
,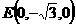
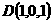 ,
,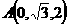
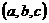 ,
,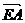

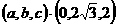

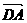
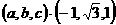
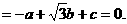

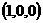 .
.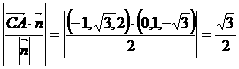
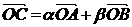 ,其中α、β∈R,且α+β=1,则点C的轨迹方程为_________________.
,其中α、β∈R,且α+β=1,则点C的轨迹方程为_________________.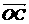 =(x,y),
=(x,y),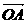 =(3,1),
=(3,1),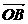 =(-1,3),α
=(-1,3),α