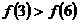考点一:求导公式。
例1. 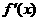 是
是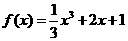 的导函数,则
的导函数,则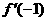 的值是
。
的值是
。
解析: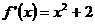 ,所以
,所以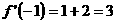
答案:3
点评:本题考查多项式的求导法则。
考点二:导数的几何意义。
例2. 已知函数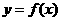 的图象在点
的图象在点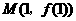 处的切线方程是
处的切线方程是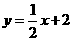 ,则
,则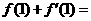 。
。
解析:因为 ,所以
,所以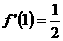 ,由切线过点
,由切线过点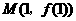 ,可得点M的纵坐标为
,可得点M的纵坐标为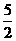 ,所以
,所以 ,所以
,所以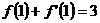
答案:3
例3.曲线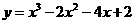 在点
在点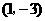 处的切线方程是
。
处的切线方程是
。
解析: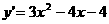 ,
, 点
点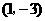 处切线的斜率为
处切线的斜率为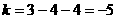 ,所以设切线方程为
,所以设切线方程为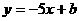 ,将点
,将点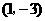 带入切线方程可得
带入切线方程可得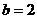 ,所以,过曲线上点
,所以,过曲线上点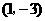 处的切线方程为:
处的切线方程为: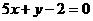
答案: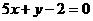
点评:以上两小题均是对导数的几何意义的考查。
考点三:导数的几何意义的应用。
例4.已知曲线C: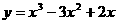 ,直线
,直线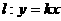 ,且直线
,且直线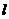 与曲线C相切于点
与曲线C相切于点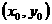
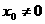 ,求直线
,求直线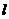 的方程及切点坐标。
的方程及切点坐标。
解析: 直线过原点,则
直线过原点,则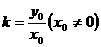 。由点
。由点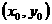 在曲线C上,则
在曲线C上,则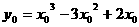 ,
,
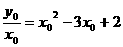 。又
。又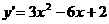 ,
, 在
在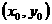 处曲线C的切线斜率为
处曲线C的切线斜率为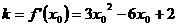 ,
,
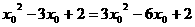 ,整理得:
,整理得: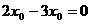 ,解得:
,解得: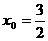 或
或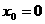 (舍),此时,
(舍),此时,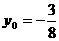 ,
,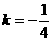 。所以,直线
。所以,直线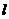 的方程为
的方程为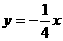 ,切点坐标是
,切点坐标是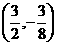 。
。
答案:直线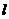 的方程为
的方程为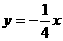 ,切点坐标是
,切点坐标是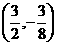
点评:本小题考查导数几何意义的应用。解决此类问题时应注意“切点既在曲线上又在切线上”这个条件的应用。函数在某点可导是相应曲线上过该点存在切线的充分条件,而不是必要条件。
考点四:函数的单调性。
例5.已知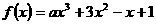 在R上是减函数,求
在R上是减函数,求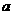 的取值范围。
的取值范围。
解析:函数 的导数为
的导数为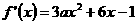 。对于
。对于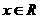 都有
都有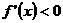 时,
时, 为减函数。由
为减函数。由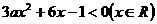 可得
可得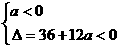 ,解得
,解得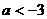 。所以,当
。所以,当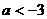 时,函数
时,函数 对
对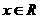 为减函数。
为减函数。
2
当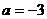 时,
时,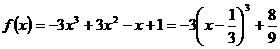 。
。
由函数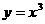 在R上的单调性,可知当
在R上的单调性,可知当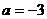 是,函数
是,函数 对
对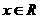 为减函数。
为减函数。
7
当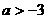 时,函数
时,函数 在R上存在增区间。所以,当
在R上存在增区间。所以,当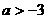 时,函数
时,函数 在R上不是单调递减函数。
在R上不是单调递减函数。
综合(1)(2)(3)可知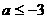 。
。
答案: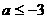
点评:本题考查导数在函数单调性中的应用。对于高次函数单调性问题,要有求导意识。
考点五:函数的极值。
例6. 设函数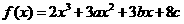 在
在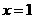 及
及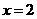 时取得极值。
时取得极值。
(1)求a、b的值;
(2)若对于任意的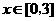 ,都有
,都有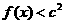 成立,求c的取值范围。
成立,求c的取值范围。
解析:(1)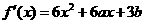 ,因为函数
,因为函数 在
在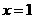 及
及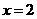 取得极值,则有
取得极值,则有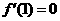 ,
,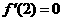 .即
.即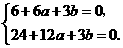 ,解得
,解得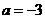 ,
,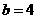 。
。
(2)由(Ⅰ)可知, ,
,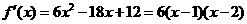 。
。
当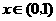 时,
时,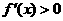 ;当
;当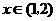 时,
时,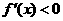 ;当
;当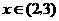 时,
时,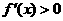 。所以,当
。所以,当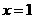 时,
时, 取得极大值
取得极大值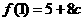 ,又
,又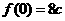 ,
,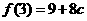 。则当
。则当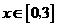 时,
时, 的最大值为
的最大值为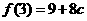 。因为对于任意的
。因为对于任意的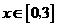 ,有
,有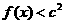 恒成立,
恒成立,
所以 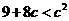 ,解得
,解得 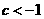 或
或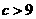 ,因此
,因此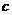 的取值范围为
的取值范围为 。
。
答案:(1)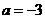 ,
,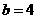 ;(2)
;(2) 。
。
点评:本题考查利用导数求函数的极值。求可导函数 的极值步骤:①求导数
的极值步骤:①求导数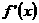 ;
;
②求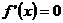 的根;③将
的根;③将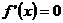 的根在数轴上标出,得出单调区间,由
的根在数轴上标出,得出单调区间,由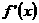 在各区间上取值的正负可确定并求出函数
在各区间上取值的正负可确定并求出函数 的极值。
的极值。
考点六:函数的最值。
例7. 已知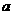 为实数,
为实数, 。求导数
。求导数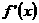 ;(2)若
;(2)若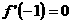 ,求
,求 在区间
在区间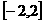 上的最大值和最小值。
上的最大值和最小值。
解析:(1)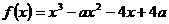 ,
,
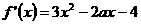 。
。
(2)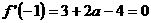 ,
,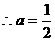 。
。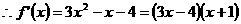
令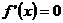 ,即
,即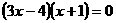 ,解得
,解得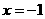 或
或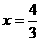 , 则
, 则 和
和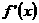 在区间
在区间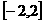 上随
上随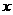 的变化情况如下表:
的变化情况如下表:
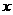 |
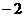 |
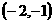 |
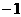 |
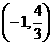 |
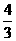 |
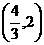 |
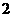 |
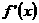 |
|
+ |
0 |
- |
0 |
+ |
|
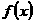 |
0 |
增函数 |
极大值 |
减函数 |
极小值 |
增函数 |
0 |
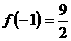 ,
,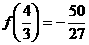 。所以,
。所以, 在区间
在区间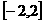 上的最大值为
上的最大值为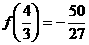 ,最小值为
,最小值为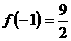 。
。
答案:(1)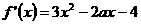 ;(2)最大值为
;(2)最大值为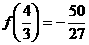 ,最小值为
,最小值为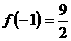 。
。
点评:本题考查可导函数最值的求法。求可导函数 在区间
在区间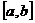 上的最值,要先求出函数
上的最值,要先求出函数 在区间
在区间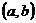 上的极值,然后与
上的极值,然后与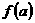 和
和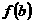 进行比较,从而得出函数的最大最小值。
进行比较,从而得出函数的最大最小值。
考点七:导数的综合性问题。
例8. 设函数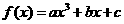
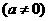 为奇函数,其图象在点
为奇函数,其图象在点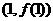 处的切线与直线
处的切线与直线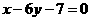 垂直,导函数
垂直,导函数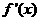 的最小值为
的最小值为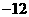 。(1)求
。(1)求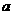 ,
,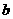 ,
,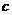 的值;
的值;
(2)求函数 的单调递增区间,并求函数
的单调递增区间,并求函数 在
在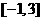 上的最大值和最小值。
上的最大值和最小值。
解析: (1)∵ 为奇函数,∴
为奇函数,∴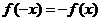 ,即
,即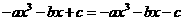
∴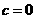 ,∵
,∵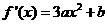 的最小值为
的最小值为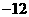 ,∴
,∴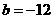 ,又直线
,又直线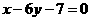 的斜率为
的斜率为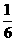 ,因此,
,因此,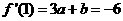 ,∴
,∴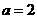 ,
,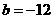 ,
,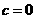 .
.
(2)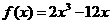 。
。 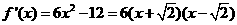 ,列表如下:
,列表如下:
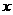 |
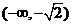 |
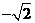 |
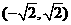 |
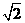 |
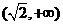 |
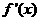 |
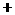 |
 |
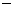 |
 |
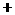 |
 |
增函数 |
极大 |
减函数 |
极小 |
增函数 |
所以函数 的单调增区间是
的单调增区间是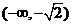 和
和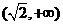 ,∵
,∵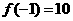 ,
,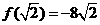 ,
,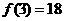 ,∴
,∴ 在
在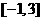 上的最大值是
上的最大值是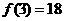 ,最小值是
,最小值是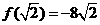 。
。
答案:(1)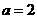 ,
,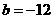 ,
,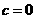 ;(2)最大值是
;(2)最大值是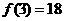 ,最小值是
,最小值是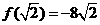 。
。
点评:本题考查函数的奇偶性、单调性、二次函数的最值、导数的应用等基础知识,以及推理能力和运算能力。
3 方法总结与2008年高考预测
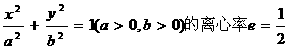 ,右焦点F(c,0),方程
,右焦点F(c,0),方程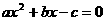 的两个根分别为x1,x2,则点P(x1,x2)在( )
的两个根分别为x1,x2,则点P(x1,x2)在( )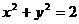 内 B.圆
内 B.圆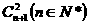 ,则
,则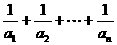 等于( )
等于( ) B.
B.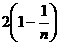 C.2-
C.2- D.1-
D.1-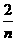
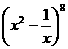 的展开式中,含x的项的系数是( )
的展开式中,含x的项的系数是( )
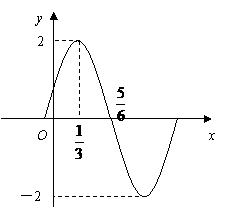
 的图象(部分)如图所示,则
的图象(部分)如图所示,则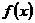 的解析式是( )
的解析式是( )

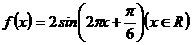
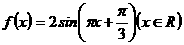

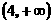 上为减函数,且函数
上为减函数,且函数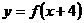 为偶函数,则( )
为偶函数,则( )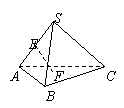 A.
A.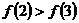 B.
B.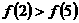 C.
C.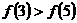 D.
D.