摘要：例3.设F是椭圆的右焦点.且椭圆上至少有21个不同的点Pi.使|FP1|.|FP2|.|FP3|.-组成公差为d的等差数列.则d的取值范围为 . 解析:由椭圆第二定义知.这些线段长度的最小值为右焦点到右顶点的距离即|FP1|=.最大值为右焦点到左顶点的距离即|FP21|=.故若公差d>0,则同理若公差d<0,则可求得. 评析:本题很好地将数列与椭圆的有关性质结合在一起.形式新颖.内容深遂.有一定的难度.可见命题设计者的良苦用心.解决的关键是确定该数列的最大项.最小项.然后根据数列的通项公求出公差的取值范围.
网址：http://m.1010jiajiao.com/timu3_id_516757[举报]
已知点F是椭圆
的右焦点，点M(m，0)、N(0，n)分别是x轴、y轴上的动点，且满足
．若点P满足
．
(Ⅰ)求点P的轨迹C的方程；
(Ⅱ)设过点F任作一直线与点P的轨迹交于A、B两点，直线OA、OB与直线x＝－a分别交于点S、T(O为坐标原点)，试判断
是否为定值？若是，求出这个定值；若不是，请说明理由．
的右焦点，过点E（2，0）且斜率为k的直线l与D交于A、B两点，C是点A关于x轴的对称点。
，求△ABC外接圆的方程。椭圆
的离心率
A、B是椭圆上关于x、y轴均不对称的两点，线段AB的垂直平分线与x轴交于点P（1，0）.
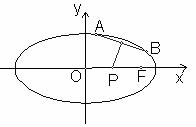
（1）设AB的中点为C（x0，y0），求x0的值;
（2）若F是椭圆的右焦点，且|AF|+|BF|=3，求椭圆的方程.
查看习题详情和答案>>
、
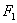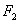分别是椭圆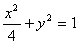
的左．右焦点．
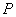是该椭圆上的一个动点，求
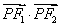的取值范围; 
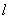与椭圆交于不同的两点M．N，且∠
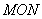为锐角（其中
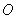为坐标原点），求直线
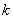的取值范围．
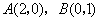是它的两个顶点，直线
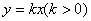与AB相交于点D，与椭圆相交于E．F两点．求四边形
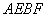面积的最大值．
的右焦点，过点E(2，0)且斜率为k(k＞0)的直线l与D交于A、B两点，C是点A关于x轴的对称点．
·
＝1，求△ABC外接圆的方程．