0 51661 51669 51675 51679 51685 51687 51691 51697 51699 51705 51711 51715 51717 51721 51727 51729 51735 51739 51741 51745 51747 51751 51753 51755 51756 51757 51759 51760 51761 51763 51765 51769 51771 51775 51777 51781 51787 51789 51795 51799 51801 51805 51811 51817 51819 51825 51829 51831 51837 51841 51847 51855 447348
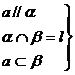
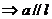
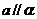 ,
,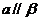 ,
, ,求证:
,求证: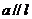 。
。 作
作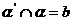
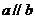
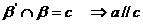
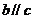
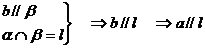
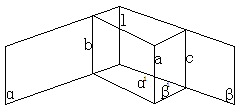
 异面,求证过
异面,求证过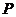 作直线
作直线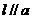
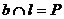 确立平面
确立平面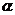
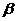 ,
,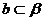 ,
,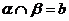
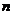 个。
个。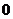 个或
个或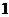 个,过
个,过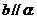 。
。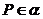 或
或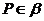
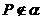 且
且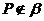
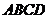 交正方形
交正方形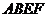 于
于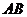 ,
,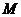 、
、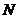 在对角线
在对角线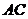 、
、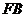 上,且
上,且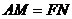 ,求证:
,求证: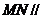 平面
平面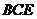 。
。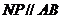 交
交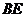 于
于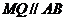 交
交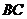 于
于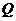
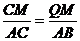 ,
,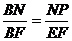
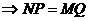
 又∵
又∵ 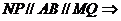
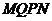
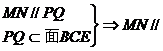 面
面
 ,
,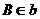 ,
,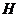 为
为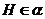 ,
,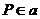 ,
,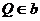 ,
,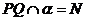 ,求:
,求: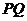 中点。
中点。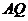 交
交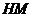 、
、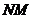
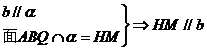
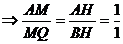
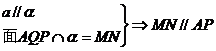
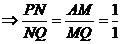
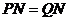
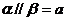 ,
,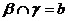 ,
,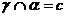
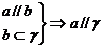
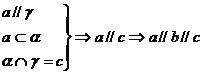
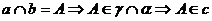
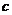 交于一点
交于一点 [例7]
[例7] 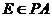 ,
,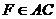 ,且
,且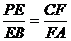 ,求证:
,求证: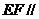 面
面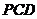 。
。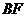 交
交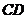 于
于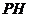 ,
,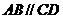
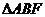 ∽
∽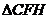
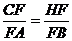
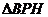 中,
中,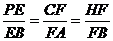
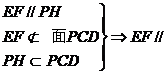 面
面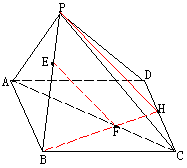
 与
与
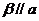
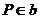 ,有无数条
,有无数条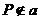 且
且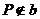
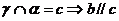
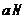
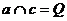
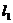 、
、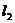 与
与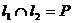 ,确立平面
,确立平面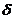
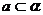
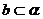 ,与
,与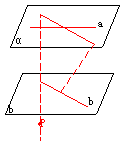
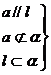
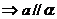
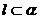 ,直线在平面内,有无数个公共点,
,直线在平面内,有无数个公共点,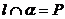 ,直线与平面相交,只有一个公共点。
,直线与平面相交,只有一个公共点。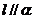 ,直线与平面平行,无公共点。
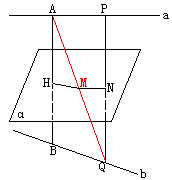
,直线与平面平行,无公共点。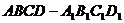 中
中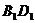 、
、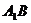 上的点且
上的点且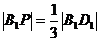 ,
,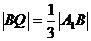 (如图甲)。求证:PQ//平面
(如图甲)。求证:PQ//平面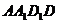
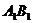 、
、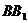 的中点(如图乙),求直线AM与CN所成的角
的中点(如图乙),求直线AM与CN所成的角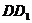 上能否找到一点H,使
上能否找到一点H,使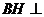 平面
平面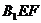 ?若能,试确定点H的位置,若不能,请说明理由。
?若能,试确定点H的位置,若不能,请说明理由。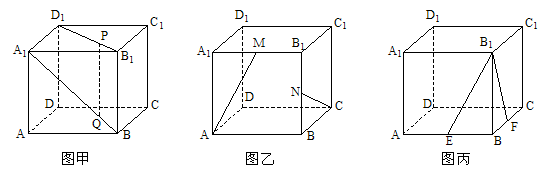
 所在平面外一点,O是边AC的中点,
所在平面外一点,O是边AC的中点,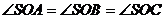 ,点P是SA的中点。
,点P是SA的中点。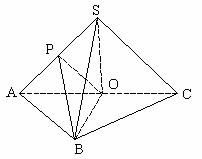
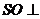 平面ABC
平面ABC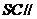 平面BOP
平面BOP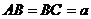 ,又SC与平面BOP的距离为
,又SC与平面BOP的距离为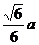 ,求二面角
,求二面角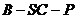 的大小。
的大小。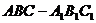 中,
中,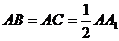 ,
,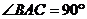 ,D为棱
,D为棱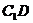 与
与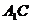 所成的角;
所成的角;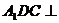 平面ADC
平面ADC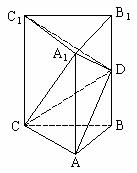
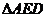 折起,使二面角
折起,使二面角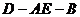 为
为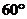 。
。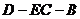 的大小
的大小
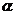 、
、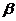 是两个不同的平面,
是两个不同的平面,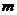 ,
,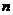 是平面
是平面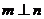 ;②
;② 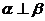 ;③
;③ 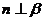 ;④
;④ 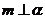 。以其中三个论断作为条件,余下的一个论断作为结论,写出你认为正确的一个命题:
。
。以其中三个论断作为条件,余下的一个论断作为结论,写出你认为正确的一个命题:
。