网址:http://m.1010jiajiao.com/timu3_id_516474[举报]
某港口海水的深度 (米)是时间
(米)是时间 (时)(
(时)( )的函数,记为:
)的函数,记为:
已知某日海水深度的数据如下:
|
|
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
|
10.0 |
13.0 |
9.9 |
7.0 |
10.0 |
13.0 |
10.1 |
7.0 |
10.0 |
经长期观察, 的曲线可近似地看成函数
的曲线可近似地看成函数 的图象
的图象
(I)试根据以上数据,求出函数 的振幅、最小正周期和表达式;
的振幅、最小正周期和表达式;
(II)一般情况下,船舶航行时,船底离海底的距离为 米或
米或 米以上时认为是安全的(船舶停靠时,船底只需不碰海底即可)。某船吃水深度(船底离水面的距离)为
米以上时认为是安全的(船舶停靠时,船底只需不碰海底即可)。某船吃水深度(船底离水面的距离)为 米,如果该船希望在同一天内安全进出港,请问,它至多能在港内停留多长时间(忽略进出港所需时间)
米,如果该船希望在同一天内安全进出港,请问,它至多能在港内停留多长时间(忽略进出港所需时间)
【解析】第一问中利用三角函数的最小正周期为:
T=12 振幅:A=3,b=10,

 第二问中,该船安全进出港,需满足:
第二问中,该船安全进出港,需满足: 即:
即:
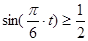 ∴
∴ 又
又  ,可解得结论为
,可解得结论为 或
或 得到。
得到。
查看习题详情和答案>>
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
|
零件的个数x(个) |
2 |
3 |
4 |
5 |
|
加工的时间y(小时) |
2.5 |
3 |
4 |
4.5 |
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程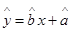 ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工10个零件需要多少时间?
(注: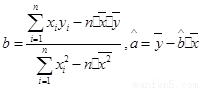 )
)
【解析】第一问中利用数据描绘出散点图即可
第二问中,由表中数据得 =52.5,
=52.5, 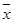 =3.5,
=3.5, =3.5,
=3.5,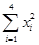 =54,∴
=54,∴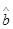 =0.7,
=0.7,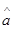 =1.05得到回归方程。
=1.05得到回归方程。
第三问中,将x=10代入回归直线方程,得y=0.7×10+1.05=8.05(小时)得到结论。
(1)散点图如下图.
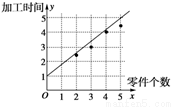 ………………4分
………………4分
(2)由表中数据得 =52.5,
=52.5, 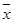 =3.5,
=3.5, =3.5,
=3.5,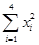 =54,
=54,
∴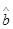 =…=0.7,
=…=0.7,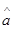 =…=1.05.
=…=1.05.
∴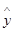 =0.7x+1.05.回归直线如图中所示.………………8分
=0.7x+1.05.回归直线如图中所示.………………8分
(3)将x=10代入回归直线方程,得y=0.7×10+1.05=8.05(小时),
∴预测加工10个零件需要8.05小时
查看习题详情和答案>>