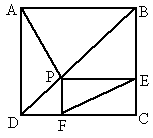
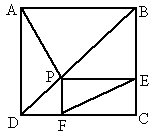
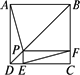
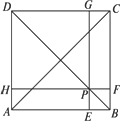
摘要：例1．如图.P是正方形ABCD的对角线BD上一点.PECF是矩形. 证明:①PA=EF ②PA⊥EF 分析:如果用平面几何的常规证法来处理这两个结论. 由于P点的不确定性.显然对大部分学生来讲很困难. 而如果抓住向量.那么可以把几何关系快速转化为数量 关系.从而通过定量分析得出定性的结果 证明:①以DC所在直线为x轴.以DA所在直线为y轴建 立如图所示的直角坐标系. 设正方形边长为1. . 则A.P.E.F ∴ ∴ ∴ ∴PA=EF ②∵ ∴ ∴PA⊥EF 例2．如图.设G是△OAB的重心.过G的直线与OA.OB分别交于P和Q.已知.△OAB和△OPQ的面积分别为S和T. 求证:(1) (2) 证明:(1)连结OG并延长交AB于M 则M为AB的中点.设a.b ∴ 又a .b ∴=kb-h a ―h a=a+b ∵P.G.Q三点共线.∴存在实数使得 即a+b=b-a 由平面向量基本定理知:消去得 (2)∵∠POQ=∠AOB ∴ 由(1)知 由于 ∴ ∴ 从而 ∴ 又∵ ∴ 综上所述:∴ 即 说明:解本题的关键是理解向量的各种运算的定义.并能熟练应用运算法则.利用向量解平面几何问题有时特别方便.但要注意一点.不宜搞得过难过深.因为高考在这方面要求不高.只是在数学竞赛中有较高要求.

网址：http://m.1010jiajiao.com/timu3_id_516472[举报]