19、(14分)已知直线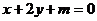
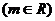 与抛物线
与抛物线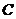 :
: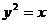 相交于不同的两点A,B
相交于不同的两点A,B
(I)求实数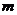 的取值范围;
的取值范围;
(II)在抛物线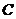 上是否存在一个定点
上是否存在一个定点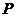 ,对(I)中任意的
,对(I)中任意的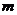 的值,都有直线
的值,都有直线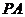 与
与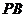 的斜率互为相反数?若存在,求出点
的斜率互为相反数?若存在,求出点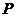 的坐标;若不存在,试说明理由
的坐标;若不存在,试说明理由
 学校_________________班级
姓名
学号 学校_________________班级
姓名
学号
|
19、(14分)已知直线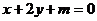
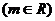 与抛物线
与抛物线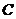 :
: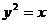 相交于不同的两点A,B
相交于不同的两点A,B
(I)求实数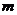 的取值范围;
的取值范围;
(II)在抛物线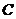 上是否存在一个定点
上是否存在一个定点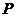 ,对(I)中任意的
,对(I)中任意的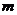 的值,都有直线
的值,都有直线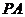 与
与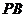 的斜率互为相反数?若存在,求出点
的斜率互为相反数?若存在,求出点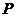 的坐标;若不存在,试说明理由
的坐标;若不存在,试说明理由
 学校_________________班级
姓名
学号 学校_________________班级
姓名
学号
|