 |
2 |
3 |
4 |
6 |
7 |
10 |
P(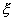 ) ) |
0.09 |
0.24 |
0.16 |
0.18 |
0.24 |
0.09 |
20、(本题满分14分)
设a>0,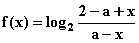 是奇函数。
(1)试确定a的值;
(2)试判断f(x)的反函数f-1(x)的单调性,并证明。
解:
(1)∵ f(x)为奇函数, ∴ f(x)+f(-x)=0
即
是奇函数。
(1)试确定a的值;
(2)试判断f(x)的反函数f-1(x)的单调性,并证明。
解:
(1)∵ f(x)为奇函数, ∴ f(x)+f(-x)=0
即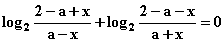 对定义域内x均成立,
解得a=1,即
对定义域内x均成立,
解得a=1,即  。
(2)由
。
(2)由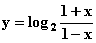 得
得 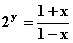 , ∴
, ∴ 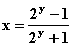 ,
∴
,
∴ 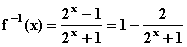 , ∴ f-1(x)在定义域内为增函数,
当任取定义域内x1,x2且x1<x2时,
因
, ∴ f-1(x)在定义域内为增函数,
当任取定义域内x1,x2且x1<x2时,
因 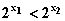 得
得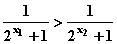 ,
则
,
则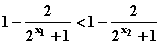 ,
∴ f-1(x1)<f-1(x2),即f-1(x)为增函数。
21、(本题满分14分)
一条斜率为1的直线l与离心率
,
∴ f-1(x1)<f-1(x2),即f-1(x)为增函数。
21、(本题满分14分)
一条斜率为1的直线l与离心率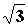 的双曲线
的双曲线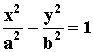 (a>0,
b>0)交于P、Q两点,直线l与y轴交于R点,且
(a>0,
b>0)交于P、Q两点,直线l与y轴交于R点,且 ,求直线和双曲线方程。
解:∵
,求直线和双曲线方程。
解:∵ 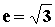 , ∴ b2=2a2,∴ 双曲线方程可化为2x2-y2=2a2,
设直线方程为 y=x+m,
由
, ∴ b2=2a2,∴ 双曲线方程可化为2x2-y2=2a2,
设直线方程为 y=x+m,
由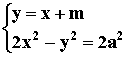 得 x2-2mx-m2-2a2=0,
∴ Δ=4m2+4(m2+2a2)>0
∴ 直线一定与双曲线相交。
设P(x1, y1), Q(x2, y2), 则x1+x2=2m,
x1x2=-m2-2a2,
∵
得 x2-2mx-m2-2a2=0,
∴ Δ=4m2+4(m2+2a2)>0
∴ 直线一定与双曲线相交。
设P(x1, y1), Q(x2, y2), 则x1+x2=2m,
x1x2=-m2-2a2,
∵ 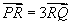 ,
, 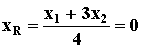 ,
∴
,
∴ 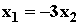 , ∴
, ∴ 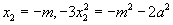 消去x2得,m2=a2,
消去x2得,m2=a2,
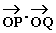 =x1x2+y1y2=x1x2+(x1+m)(x2+m)
=2x1x2+m(x1+x2)+m2=m2-4a2=-3
∴ m=±1, a2=1, b2=2.
直线方程为y=x±1,双曲线方程为
=x1x2+y1y2=x1x2+(x1+m)(x2+m)
=2x1x2+m(x1+x2)+m2=m2-4a2=-3
∴ m=±1, a2=1, b2=2.
直线方程为y=x±1,双曲线方程为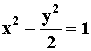 。
。
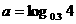 ,
,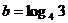 ,
,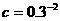 ,则
,则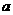 、
、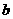 、
、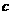 的大小关系为( )
的大小关系为( )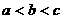 B.
B.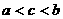 C.
C.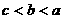 D.
D.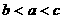
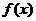 是奇函数,
是奇函数,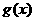 是偶函数,且
是偶函数,且 ,则
,则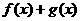 等于( )
等于( )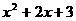 B.
B.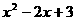 C.
C.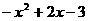 D.
D.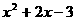
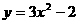 在区间
在区间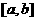 上有最小值
上有最小值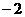 ,则下列关系式中一定成立的是( )
,则下列关系式中一定成立的是( )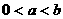 或
或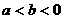 B.
B.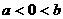
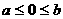
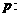 不等式
不等式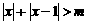 的解集为
的解集为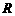 ,
,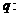
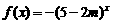 是减函数,则
是减函数,则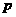 是
是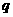 的( )
的( )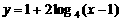 ,则
,则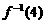 的值是( )
的值是( )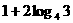 B.
B.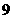 C.
C.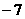 D.
D.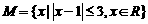 ,
,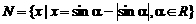 ,则
,则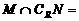 ( )
( )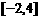 B.
B.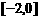 C.
C.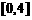 D.
D.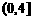
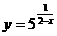 B.
B.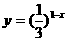 C.
C.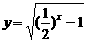 D.
D.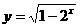
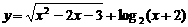 的定义域为( )
的定义域为( ) B.
B.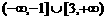 C.
C.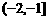 D.
D.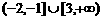
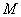 ;
(Ⅱ)分别求随机变量
;
(Ⅱ)分别求随机变量