直线定理可知PN⊥l, ∴∠PNH是二面角α-l-β的平面角,即∠PNH=45°.
设PQ=x,则NH=PH=xsin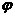 ,
,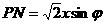 ,MN=NH·cotθ=xsin
,MN=NH·cotθ=xsin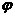 ·cotθ.
·cotθ.
在Rt△PMN中,∵PM2=PN2+MN2,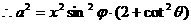 ,故
,故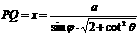 .
.
|
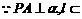 α,l⊥AC,∴l⊥PC即PC是P到l的距离.
α,l⊥AC,∴l⊥PC即PC是P到l的距离.
|
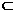 β,l⊥PC,∴l⊥BC. 即∠ACB为二面角α-l-β的平面角,∠ACB=θ,
β,l⊥PC,∴l⊥BC. 即∠ACB为二面角α-l-β的平面角,∠ACB=θ,
∵l⊥AC,l⊥PC,l⊥BC, ∴PACB是一个平面四边形. 又∠PAC=∠PBC=90°,∴四边形PACB内
接于以PC为直径的圆,∠APB=π-θ. 在△APB中,由余弦定理,得 AB2=PA2+PB2-2PA·PBcos
∠APB=m2+n2+2mncosθ. 由正弦定理,得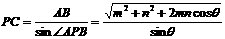 ,即为所求P到
,即为所求P到
l的距离.
(21)(Ⅰ)∵∠BAC=∠CAD=∠DAB=60°, AC=AD=2,AB=3, ∴△ABC≌△ABD,BC=BD.
取CD的中点M,连AM、BM,则CD⊥AM,CD⊥BM. ∴CD⊥平面ABM,于是AB⊥BD.
(Ⅱ)由CD⊥平面ABM,则平面ABM⊥平面BCD,这样∠ABM是AB与平面BCD所成的角.
在△ABC中,AB=3,AC=2,∠BAC=60°,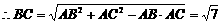 . 在△ACD中,
. 在△ACD中,
AC=AD=2,∠CAD=60°,∴△ACD是正三角形,AM=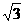 . 在Rt△BCM中,BC=
. 在Rt△BCM中,BC=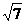 ,CM=1,
,CM=1,
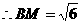 .
.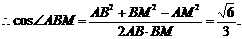
(22)(Ⅰ)延长ED交CB延长线于F,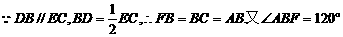
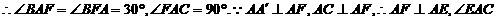 为截
为截
面与底面所成二面角的平面角. 在Rt△AEC中,EC=AC,故得∠EAC=45°.
(Ⅱ)设AB=a,则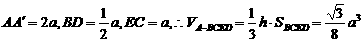 ,
,
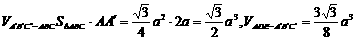 .
. 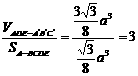
(23)S底面=S△ABD·cos30°,设底面边长为x,则有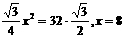 .取AB中点E,在Rt△DEC中,
.取AB中点E,在Rt△DEC中,
∠DEC=30°,故
(24)(Ⅰ)在△ABC中,AB=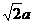 ,BC=AC=a,∴△ABC是等腰直角三角形,BC⊥AC,∠CAB=45°,
,BC=AC=a,∴△ABC是等腰直角三角形,BC⊥AC,∠CAB=45°,
又BC⊥A1O,故BC⊥侧面AC1,AB与侧面AC1所成角就是∠BAC=45°.
(Ⅱ)由(Ⅰ)知四边形B1BCC1为矩形,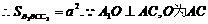 中点,
中点,
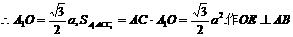 于E,连结A1E,则AB⊥A1E. 在Rt△AOE
于E,连结A1E,则AB⊥A1E. 在Rt△AOE
中,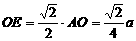 ,在Rt△A1EO中,
,在Rt△A1EO中,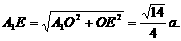
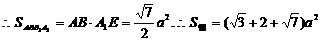 .
.
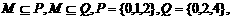 则满足上述条件的集合M的个数是( )
则满足上述条件的集合M的个数是( )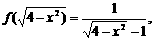 则
则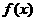 的定义域是 ( )
的定义域是 ( ) (D)
(D)
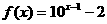 ,则
,则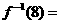 ( )
( )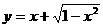 的最大值和最小值分别是 ( )
的最大值和最小值分别是 ( ) (B)1,-1 (C)
(B)1,-1 (C)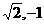 (D)
(D)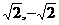
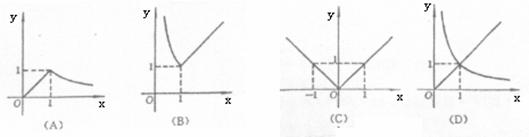 (5)函数
(5)函数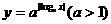 的图象是 ( )
的图象是 ( )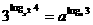 的解集是 ( )
的解集是 ( )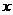 方程
方程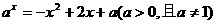 的解的个数是 ( )
的解的个数是 ( ) (B)
(B)
 (D)
(D)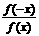
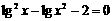 的两根是α、β,则
的两根是α、β,则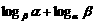 的值是 ( )
的值是 ( )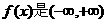 上的奇函数,
上的奇函数,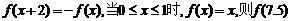 =
=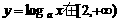 上恒有|y|>1,则a的取值范围是 ( )
上恒有|y|>1,则a的取值范围是 ( )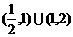 (B)
(B)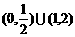 (C)(1,2) (D)
(C)(1,2) (D)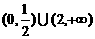
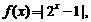 若a<b<c,且
若a<b<c,且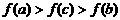 ,则下面四个式子中成立的是
,则下面四个式子中成立的是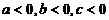 (B)
(B)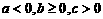
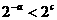 (D)
(D)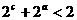
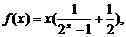 求证对任意
求证对任意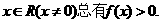
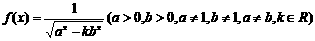 的定义域.
的定义域.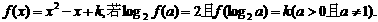
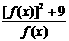 的最小值及对应的x值.
的最小值及对应的x值.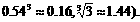
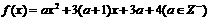 的图象过点(m-2,0),m∈R,设g(x)=
的图象过点(m-2,0),m∈R,设g(x)= 问是否存在实数p(p<0
问是否存在实数p(p<0 ,使F(x)在(-∞,―3)
,使F(x)在(-∞,―3)
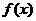 的定义域、值域及其反函数
的定义域、值域及其反函数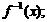
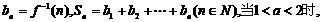 试比较
试比较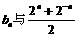 的大
的大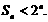
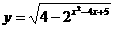 的定义域是
,值域是
.
的定义域是
,值域是
.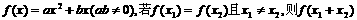 = .
= .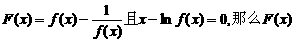 是 ( )
是 ( ) 平移,使曲线上点P的坐标由(1,0)变为(2,2),则此曲线平移
平移,使曲线上点P的坐标由(1,0)变为(2,2),则此曲线平移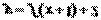 (B)
(B)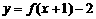
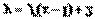 (D)
(D)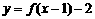
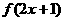 是偶函数,则函数
是偶函数,则函数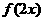 的图象的对称轴是 ( )
的图象的对称轴是 ( ) (B)x=1 (C)
(B)x=1 (C) (D)
(D)
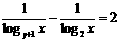 的图象是 ( )
的图象是 ( )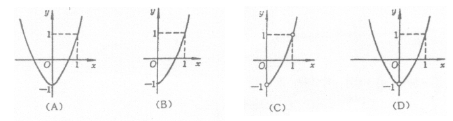
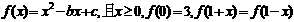 则有 ( )
则有 ( )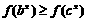 (B)
(B)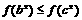
 (D)
(D)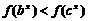
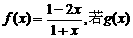 的图象与
的图象与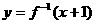 的图象关于直线
的图象关于直线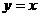 对称,
对称,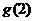 值等于 ( )
值等于 ( )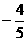 (D)
(D)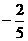
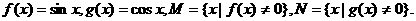 那么
那么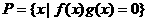 应为 ( )
应为 ( )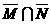 (B)
(B) (C)
(C)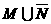 (D)
(D)
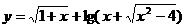 的最小值为 ( )
的最小值为 ( )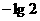 (B)
(B)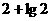 (C)
(C)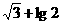 (D)不存在
(D)不存在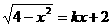 只有一个实数根,则k的值为 ( )
只有一个实数根,则k的值为 ( )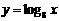 的图象交于A、B两点,
的图象交于A、B两点,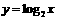 的图象交于C、D两点,可以证明直线AB与
的图象交于C、D两点,可以证明直线AB与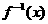 ,把
,把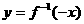 (B)
(B)
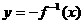 (D)
(D)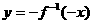
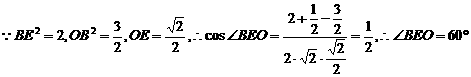 ;
;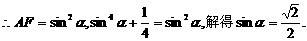
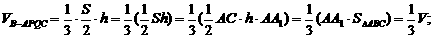
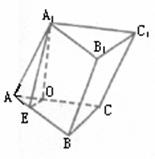 24.如图,在三棱柱ABC-A1B1C1中,AB=
24.如图,在三棱柱ABC-A1B1C1中,AB=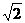 a,BC=CA=AA1=a,A1在底面ABC上的
a,BC=CA=AA1=a,A1在底面ABC上的