(1)已知集合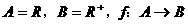 是从集合A到B的一个映射,若
是从集合A到B的一个映射,若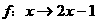 ,则B中的元素3的原象为
,则B中的元素3的原象为
(A)-1 (B)1 (C)2 (D)3
(2)已知两条直线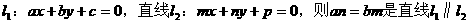 的
的
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
(3) (t是参数,t∈R)表示的曲线的对称轴的方程是
(t是参数,t∈R)表示的曲线的对称轴的方程是
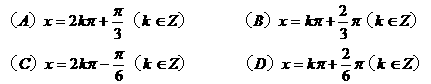
(4)在复平面中,已知点A(2,1),B(0,2),C(-2,1),O(0,0)。给出下面的结论:
①直线OC与直线BA平行; ②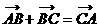 ;
;
③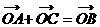 ;
④
;
④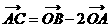 。
。
其中正确结论的个数是
(A)1个 (B)2个 (C)3个 (D)4个
(5)圆锥的侧面积为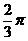 ,侧面展开图的圆心角为
,侧面展开图的圆心角为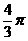 ,则此圆锥的体积为
,则此圆锥的体积为
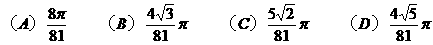
(6)已知数列 ,其中a、b均为正常数,那么
,其中a、b均为正常数,那么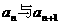 的大小关系是
的大小关系是
(A)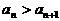 (B)
(B)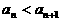 (C)
(C)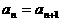 (D)与n的取值相关
(D)与n的取值相关
(7)某农贸市场出售西红柿,当价格上涨时,供给量相应增加,而需求量相应减少,具体调查结果如下表:
表1 市场供给表
|
单价(元/kg) |
2 |
2.
4 |
2.
8 |
3.
2 |
3.
6 |
4 |
|
供给量(1000kg) |
50 |
60 |
70 |
75 |
80 |
90 |
表2 市场需求表
|
单价(元/kg) |
4 |
3.
4 |
2.
9 |
2.
6 |
2.
3 |
2 |
|
需求量(1000kg) |
50 |
60 |
65 |
70 |
75 |
80 |
根据以上提供的信息,市场供需平衡点(即供给量和需求量相等时的单价)应在区间
(A)(2. 3,2. 6)内 (B)(2. 4,2. 6)内
(C)(2. 6,2. 8)内 (D)(2. 8,2. 9)内
(8)已知f(x)是R上的偶函数,且在[0,+∞)上是减函数,f(a)= 0(a>0),那么不等式xf(x)<0的解集是
(A){x | 0 < x < a} (B){x | -a < x < 0或x > a}
(A){x | -a < x < a} (D){x | x < -a或0 < x < a}
(9)双曲线的虚轴长为4,离心率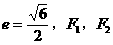 分别是它的左、右焦点,若过
分别是它的左、右焦点,若过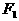 的直线与双曲线的左支交于A、B两点,且|AB|是|
的直线与双曲线的左支交于A、B两点,且|AB|是|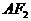 |与|
|与|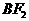 |的等差中项,则|AB|等于
|的等差中项,则|AB|等于
(A)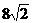 (B)
(B)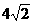
(C)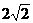 (D)8
(D)8
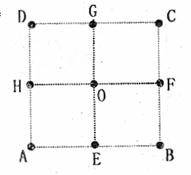
(10)如图,在正方形ABCD中,E、F、G、H是各边中点,O是正方形中心,在A、E、B、F、C、G、D、H、O这九个点中,以其中三个点为顶点作三角形,在这些三角形中,互不全等的三角形共有
(A)6个 (B)7个
(C)8个 (D)9个
第Ⅱ卷(非选择题共100分)

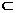 β,且α⊥β,则l⊥α.
B、若l⊥β,且α∥β,则l⊥α.
β,且α⊥β,则l⊥α.
B、若l⊥β,且α∥β,则l⊥α.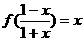 ,则下列等式正确的是
,则下列等式正确的是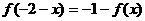 B、
B、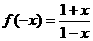
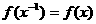 D、
D、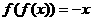
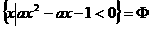 ,则实数
,则实数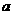 的值的集合是
的值的集合是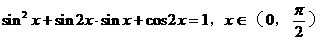 ,求tg2x的值。
,求tg2x的值。 中,E、F分别为
中,E、F分别为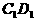 与AB的中点。
与AB的中点。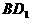 ,与CF所成角的余弦值;
,与CF所成角的余弦值;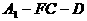 的大小。
的大小。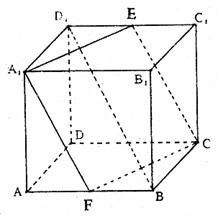
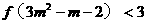 。
。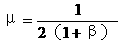 。
。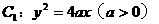 ,椭圆C以原点为中心,以抛物线
,椭圆C以原点为中心,以抛物线 的焦点为右焦点,且长轴与短轴之比为
的焦点为右焦点,且长轴与短轴之比为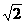 ,过抛物线
,过抛物线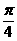 的直线l,交椭圆C于一点P(点P在x轴上方),交抛物线
的直线l,交椭圆C于一点P(点P在x轴上方),交抛物线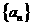 的各项均为正整数,且满足
的各项均为正整数,且满足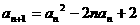 ,(n∈N),又
,(n∈N),又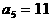 。
。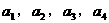 的值,并由此推测出
的值,并由此推测出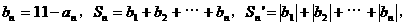 求
求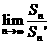 的值;
的值;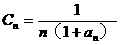 (n∈N),
(n∈N),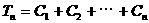 ,是否存在最大的整数m,使得对任意n∈N,均有
,是否存在最大的整数m,使得对任意n∈N,均有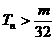 ?若存在,求出m的值;若不存在,请说明理由。
?若存在,求出m的值;若不存在,请说明理由。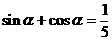 ,那么角
,那么角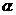 是第________象限的角。
是第________象限的角。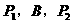 共线,
共线,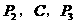 共线,且
共线,且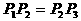 ,则在三棱锥P-ABC中,PA与BC所成的角的大小是___________。
,则在三棱锥P-ABC中,PA与BC所成的角的大小是___________。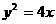 的一条弦AB以点P(1,1)为中点,则该弦所在直线斜率的值为_________。
的一条弦AB以点P(1,1)为中点,则该弦所在直线斜率的值为_________。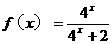 ,那么
,那么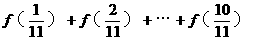 的值为_________。
的值为_________。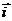 =(1,0),
=(1,0),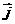 =(0,1),
=(0,1), =x
=x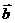 =x
=x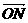 =
=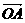 +
+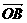 ,问是否存在直线l,使四边形OANB为矩形?若存在,求出直线l的方程;若不存在,请说明理由.
,问是否存在直线l,使四边形OANB为矩形?若存在,求出直线l的方程;若不存在,请说明理由.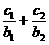 +…+
+…+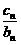 =an+1成立,求c1+c2+…+c2005的值.
=an+1成立,求c1+c2+…+c2005的值.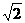 ,8]
,8]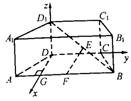 (Ⅰ)求证:EF∥平面ADD1A1;
(Ⅰ)求证:EF∥平面ADD1A1;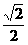 ,求A1F与平面DEF所成的角的大小.
,求A1F与平面DEF所成的角的大小.