摘要:5.解析几何 例17 如图.椭圆中心在坐标原点.F为左焦点.当⊥时. x 其离心率为.此类椭圆被称为“黄金椭圆 .类比黄金椭圆. 可推算出“黄金双曲线 的离心率e 等于 . 点通:猜想出“黄金双曲线 的离心率e 等于.事实上 对直角应用勾股定理.得 .即有 . 注意到.变形得 .从而 说明:类比推理.类比发现是今年高考的一个新的亮点.这种问题的情景比较清新.结构比较巧妙.变化比较合理.是用"活题"考能力的典范. 例18 连接抛物线上任意四点组成的四边形可能是 (填写所有正确选项的序号). ①菱形 ②有3条边相等的四边形 ③梯形 ④平行四边形 ⑤有一组对角相等的四边形 点通:①菱形不可能.如果这个四边形是菱形.那么菱形的一条对角线垂直抛物线的对称轴.这时四边形的必有一个顶点在抛物线的对称轴上,④平行四边形也不可能.因为抛物上四个点组成的四边形最多有一组对边平行.故连接抛物线上任意四点组成的四边形可能是②③⑤. 说明:针对②③⑤.你能构造出具体的图形吗?
网址:http://m.1010jiajiao.com/timu3_id_501356[举报]
(本小题满分12分)
如图,椭圆![]() 的一个焦点是F(1,0),O为坐标原点。
的一个焦点是F(1,0),O为坐标原点。

(Ⅰ)已知椭圆短轴的两个三等分点与一个焦点构成正三角形,求椭圆的方程;
(Ⅱ)设过点F的直线l交椭圆于A、B两点,若直线l绕点F任意转动,值有![]() ,求a的取值范围。
,求a的取值范围。
(08年福建卷理)(本小题满分12分)
如图,椭圆![]() 的一个焦点是
的一个焦点是![]() ,O为坐标原点.
,O为坐标原点.
(Ⅰ)已知椭圆短轴的两个三等分点与一个焦点构成正三角
形,求椭圆的方程;
(Ⅱ)设过点F的直线l交椭圆于A、B两点.若直线l绕点F
任意转动,恒有![]() ,求a的取值范围.
,求a的取值范围.

(本小题满分12分)
如图,椭圆 的一个焦点是F(1,0),O为坐标原点。
的一个焦点是F(1,0),O为坐标原点。
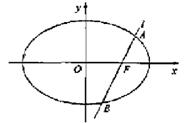
(Ⅰ)已知椭圆短轴的两个三等分点与一个焦点构成正三角形,求椭圆的方程;
(Ⅱ)设过点F的直线l交椭圆于A、B两点,若直线l绕点F任意转动,值有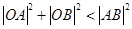 ,求a的取值范围。
,求a的取值范围。
查看习题详情和答案>>
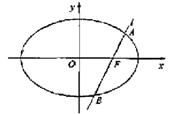
 如图,椭圆Ⅰ与Ⅱ有公共的左顶点和公共的左焦点F,且椭圆Ⅱ的右顶点为椭圆Ⅰ的中心,设椭圆Ⅰ与Ⅱ的离心率分别为e1和e2,则( )
如图,椭圆Ⅰ与Ⅱ有公共的左顶点和公共的左焦点F,且椭圆Ⅱ的右顶点为椭圆Ⅰ的中心,设椭圆Ⅰ与Ⅱ的离心率分别为e1和e2,则( )