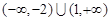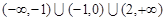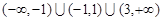摘要: 函数.不等式与导数 例1 函数的反函数 . 点通:由.得.解出.从而.从而应填. 说明:原函数的值域是反函数的定义域.求反函数的程序为:先求原函数的值域.再反解. 例2 不等式的解集是 . 点通:不等式等价于.也就是.所以.从而应填. 说明:快速解答此题需要记住小结论:应用小结论:. 例3 已知直线过点.且与轴.轴的正半轴分别交于两点.为坐标原点.则三角形面积的最小值为 . 点通:设直线为.则有关系. 对应用2元均值不等式.得.即. 于是.三角形面积为 .从而应填4. 说明:也可由.得.特别注意.不等式中的等号是可以成立的. 例4 已知a,b为常数.若则 . 点通:由f(x)=x2+4x+3, f=x2+10x+24, 得 2+4+3=x2+10x+24, 即 a2x2+2abx+b2+4ax+4b+3=x2+10x+24, 比较系数.得 解得 . 或.所以. 说明:本题考查了复合函数解析式的运用.待定系数法及其相关的计算. 例5 若函数在区间上的最大值和最小值之差为 . 点通:显然有.易知当时.函数取得最小值,当时.函数取最大值.后者与前者的差为20. 说明:三次函数是高考的一个热门话题.连续函数在闭区间上必有最大值和最小值.
网址:http://m.1010jiajiao.com/timu3_id_501352[举报]
已知定义在R上函数f(x)部分自变量与函数值对应关系如表,若f(x)为偶函数,且在[0,+∞)上为增函数,不等式-1≤f(x)<3的解集是( )
|
查看习题详情和答案>>
|
查看习题详情和答案>>
| |||||
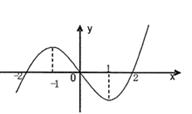
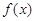 的图象如图所示,则不等式
的图象如图所示,则不等式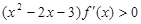 的解集为 (
)
的解集为 (
)