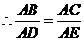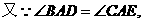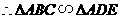0 49006 49014 49020 49024 49030 49032 49036 49042 49044 49050 49056 49060 49062 49066 49072 49074 49080 49084 49086 49090 49092 49096 49098 49100 49101 49102 49104 49105 49106 49108 49110 49114 49116 49120 49122 49126 49132 49134 49140 49144 49146 49150 49156 49162 49164 49170 49174 49176 49182 49186 49192 49200 447348
 如图,点
如图,点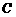 是
是 的中点,
的中点,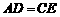 ,
,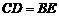 .
.  ≌△
≌△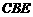
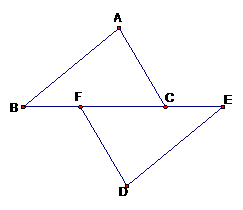
 求证:(1)OA=OB;(2)AB∥CD.
求证:(1)OA=OB;(2)AB∥CD. 中,点
中,点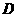 、
、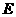 分别在边
分别在边 、
、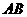 上,
上,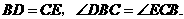 求证:
求证: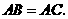
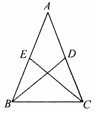
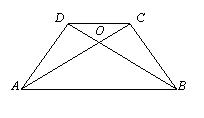
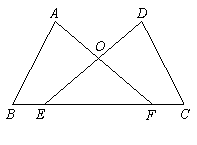 (1)求证:AB=DC;
(1)求证:AB=DC;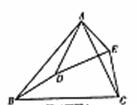 反思:对于此类证明线段或角的问题,应先从结论出发,分析证明结论所需的条件。再根据条件,选择适合的知识点进行证明。如本题要证明线段相等,根据条件,选择不同的判定,证明的方法、难易度也会因此不同。
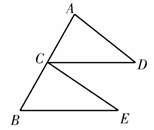
反思:对于此类证明线段或角的问题,应先从结论出发,分析证明结论所需的条件。再根据条件,选择适合的知识点进行证明。如本题要证明线段相等,根据条件,选择不同的判定,证明的方法、难易度也会因此不同。 (1)写出图中两对相似三角形(不得添加字母和线);
(1)写出图中两对相似三角形(不得添加字母和线);