摘要：实验与探究 (1)在图1.2.3中.给出平行四边形的顶点的坐标.写出图1.2.3中的顶点的坐标.它们分别是 . . , (2)在图4中.给出平行四边形的顶点的坐标.求出顶点的坐标(点坐标用含的代数式表示), 归纳与发现 (3)通过对图1.2.3.4的观察和顶点的坐标的探究.你会发现:无论平行四边形处于直角坐标系中哪个位置.当其顶点坐标为时.则四个顶点的横坐标之间的等量关系为 ,纵坐标之间的等量关系为 , 运用与推广 (4)在同一直角坐标系中有抛物线和三个点.(其中)．问当为何值时.该抛物线上存在点.使得以为顶点的四边形是平行四边形?并求出所有符合条件的点坐标． 解:(1)..．···························································· 2分 (2)分别过点作轴的垂线.垂足分别为. 分别过作于.于点． 在平行四边形中..又. ． ． 又. ．·································································································· 5分 .． 设．由.得． 由.得．．································ 7分 (此问解法多种.可参照评分) (3).或.．························· 9分 (4)若为平行四边形的对角线.由(3)可得．要使在抛物线上. 则有.即． .．此时．································································ 10分 若为平行四边形的对角线.由(3)可得.同理可得.此时． 若为平行四边形的对角线.由(3)可得.同理可得.此时． 综上所述.当时.抛物线上存在点.使得以为顶点的四边形是平行四边形． 符合条件的点有..．······················································· 12分
网址：http://m.1010jiajiao.com/timu3_id_459803[举报]
实验与探究：
（1）在图1，2，3中，已知平行四边形ABCD的三个顶点A，B，D的坐标（如图所示），求出图1，2，3中的第四个顶点C的坐标，已求出图1中顶点C的坐标是（5，2），图2，3中顶点C的坐标分别是 ， ；
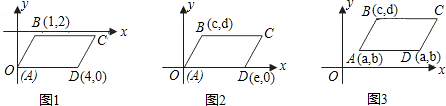
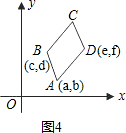
（2）在图4中，平行四边形ABCD的顶点A，B，D的坐标（如图所示），求出顶点C的坐标（C点坐标用含a，b，c，d，e，f的代数式表示）；
归纳与发现：
（3）通过对图1，2，3，4的观察和顶点C的坐标的探究，你会发现：无论平行四边形ABCD处于直角坐标系中哪个位置，当其顶点坐标为A（a，b），B（c，d），C（m，n），D（e，f）（如图4）时，则四个顶点的横坐标a，c，m，e之间的等量关系为 ；纵坐标b，d，n，f之间的等量关系为
（不必证明）；运用与推广：
（4）在同一直角坐标系中有抛物线y=x2-（5c-3）x-c和三个点G(-
c，
c)，S(
c，
c)，H（2c，0）（其中c＞0）．问当c为何值时，该抛物线上存在点P，使得以G，S，H，P为顶点的四边形是平行四边形？并求出所有符合条件的P点坐标．
查看习题详情和答案>>
（1）在图1，2，3中，已知平行四边形ABCD的三个顶点A，B，D的坐标（如图所示），求出图1，2，3中的第四个顶点C的坐标，已求出图1中顶点C的坐标是（5，2），图2，3中顶点C的坐标分别是
（2）在图4中，平行四边形ABCD的顶点A，B，D的坐标（如图所示），求出顶点C的坐标（C点坐标用含a，b，c，d，e，f的代数式表示）；
归纳与发现：
（3）通过对图1，2，3，4的观察和顶点C的坐标的探究，你会发现：无论平行四边形ABCD处于直角坐标系中哪个位置，当其顶点坐标为A（a，b），B（c，d），C（m，n），D（e，f）（如图4）时，则四个顶点的横坐标a，c，m，e之间的等量关系为
（不必证明）；运用与推广：
（4）在同一直角坐标系中有抛物线y=x2-（5c-3）x-c和三个点G(-
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
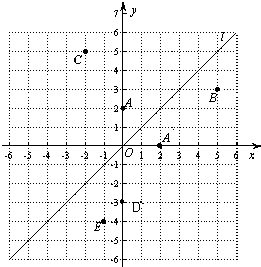
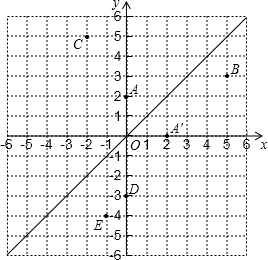如图，在平面直角坐标系中，函数y=x的图象l是第一、三象限的角平分线．（1）实验与探究：由图观察易知A（0，2）关于直线l的对称点A′的坐标为（2，0），请在图中分别标明B（5，3）、C（-2，5）关于直线l的对称点B′、C′的位置，并写出它们的坐标：B′
（3，5）
（3，5）
、C′（5，-2）
（5，-2）
；（2）归纳与发现：结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点P（m，n）关于第一、三象限的角平分线l的对称点P′的坐标为
（n，m）
（n，m）
；（3）类比与猜想：坐标平面内任一点P（m，n）关于第二、四象限的角平分线的对称点P′的坐标为
（-n，-m）
（-n，-m）
；（4）运用与拓广：已知两点D（0，-3）、E（-1，-4），试在第一、三象限的角平分线l上确定一点Q，使点Q到D、E两点的距离之和最小，并求出Q点坐标．
25、实验与探究：（1）由图观察易知A（0，2）关于直线l的对称点A′的坐标为（2，0），请在图中分别标明B（5，3）、C（-2，5）关于直线l的对称点B'、C′的位置，并写出他们的坐标：B′
（3，5）
、C′（5，-2）
；归纳与发现：
（2）结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点P（a，b）关于第一、三象限的角平分线l的对称点P'的坐标为
（b，a）
（不必证明）；运用与拓广：
（3）已知两点D（1，-3）、E（-1，-4），试在直线l上确定一点Q，使点Q到D、E两点的距离之和最小．（要有必要的画图说明，并保留作图痕迹）
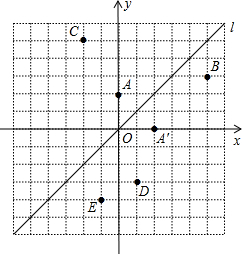
28、如图，在平面直角坐标系中，函数y=x的图象l是第一、三象限的角平分线．