摘要：如图所示.在平面直角坐标系内.点A和点C的坐标分别为(4.8).(0.5).过点A作AB⊥x轴于点B.过OB上的动点D作直线y＝kx+b平行于AC.与AB相交于点E.连结CD.过点E作EF∥CD交AC于点F. (1)求经过A.C两点的直线的解析式, (2)当点D在OB上移动时.能否使四边形CDEF成为矩形?若能.求出此时k.-b的指,若不能.请说明理由, (3)如果将直线AC作上下平移.交y轴于C’.交AB于A’.连结DC’.过点E作EF’∥DC’.交A’C’于F’.那么能否使四边形C’DEF’为正方形?若能.请求出正方形的面积,若不能.请说明理由.
网址：http://m.1010jiajiao.com/timu3_id_459802[举报]
22、如图所示，在平面直角坐标中，抛物线的顶点P到轴的距离是4，抛物线与x轴相交于O、M两点，OM=4；矩形ABCD的边BC在线段的OM上，点A、D在抛物线上．（1）请写出P、M两点坐标，并求出这条抛物线的解析式；
（2）设矩形ABCD的周长为l，求l的最大值；
（3）连接OP、PM，则△PMO为等腰三角形，请判断在抛物线上是否存在点Q（除点M外），使得△OPQ也是等腰三角形，简要说明你的理由．
如图所示，在平面直角坐标中，抛物线经过原点O与点M（-4，0），顶点N的纵坐标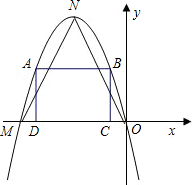
为4，以线段OM上的一个动点C为一个顶点，构造矩形ABCD，使边CD在线段OM上，点D在点C的左侧，点A、B在抛物线上
（1）连接MN、ON，求△MON的面积；
（2）求抛物线的解析式；
（3）探究：当拖动点C时，矩形ABCD的形状会发生变化
①当矩形ABCD为正方形时，求出点A的坐标；
②设矩形ABCD的周长为l，请问l是否存在一个最大值？如果存在，求出这个最大值；如果不存在，请说明理由． 查看习题详情和答案>>
为4，以线段OM上的一个动点C为一个顶点，构造矩形ABCD，使边CD在线段OM上，点D在点C的左侧，点A、B在抛物线上（1）连接MN、ON，求△MON的面积；
（2）求抛物线的解析式；
（3）探究：当拖动点C时，矩形ABCD的形状会发生变化
①当矩形ABCD为正方形时，求出点A的坐标；
②设矩形ABCD的周长为l，请问l是否存在一个最大值？如果存在，求出这个最大值；如果不存在，请说明理由． 查看习题详情和答案>>
如图所示，在平面直角坐标中，四边形OABC是等腰梯形，BC∥OA，OA=7，AB=4，
∠COA=60°，点P为x轴上的一个动点，但是点P不与点0、点A重合．连接CP，D点是线段AB上一点，连PD．
（1）求点B的坐标；
（2）当点P运动到什么位置时，△OCP为等腰三角形，求这时点P的坐标；
（3）当∠CPD=∠OAB，且
=
，求这时点P的坐标．
查看习题详情和答案>>
∠COA=60°，点P为x轴上的一个动点，但是点P不与点0、点A重合．连接CP，D点是线段AB上一点，连PD．（1）求点B的坐标；
（2）当点P运动到什么位置时，△OCP为等腰三角形，求这时点P的坐标；
（3）当∠CPD=∠OAB，且
| BD |
| AB |
| 5 |
| 8 |
（2012•包河区一模）如图所示，在平面直角坐标中，抛物线的顶点P到x轴的距离是4，抛物线与x轴相交于O、M两点，OM=4；矩形ABCD的边BC在线段OM上，点A、D在抛物线上．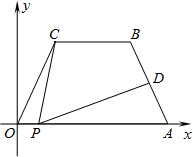
如图所示，在平面直角坐标中，四边形OABC是等腰梯形，CB∥OA，OA=7，AB=4，∠COA=60°，点P为x轴上的一个动点，点P不与点0、点A重合．连接CP，过点P作PD交AB于点D．