摘要：29． 如图.正方形ABCD的边长为12.划分成12×12个 小正方形. 将边长为n(n为整数.且2≤n≤11)的黑白 两色正方形纸片按图中的方式黑白相间地摆放.第一张 n×n的纸片正好盖住正方形ABCD左上角的n×n个小正 方形格.第二张纸片盖住第一张纸片的部分恰好为(n-1) ×(n-1)的正方形. 如此摆放下去.最后直到纸片盖住 正方形ABCD的右下角为止. 请你认真观察思考后回答下 列问题: (1)由于正方形纸片边长n的取值不同.完成摆放时所使用正方形纸 片的张数也不同.请填写下表: 纸片的边长n 2 3 4 5 6 使用的纸片张数 (2)设正方形ABCD被纸片盖住的面积为S1.未被盖住的面积为S2. ①当n=2时.求S1∶S2的值, ②是否存在使得S1=S2的n值?若存在.请求出这样的n值,若不存在.请说明理由.
网址：http://m.1010jiajiao.com/timu3_id_457853[举报]
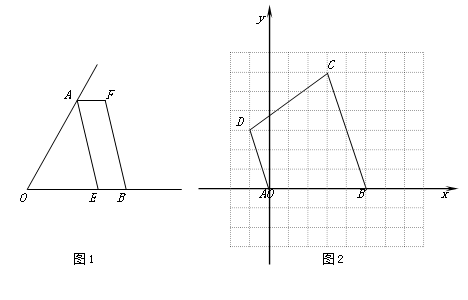
（本题满分10分）（1）如图1，已知∠AOB，OA＝OB，点E在OB边上，四边形AEBF 是平行四边形，请你只用无刻度的直尺在图中画出∠AOB的平分线．（保留作图痕迹，不要求写作法）
（2）如图2，在10×10的正方形网格中，点A（0，0）、B（5，0）、C（3，6）、D（－1，3），
①依次连结A、B、C、D四点得到四边形ABCD，四边形ABCD的形状是 ▲ .
②在x轴上找一点P，使得△PCD的周长最短（直接画出图形，不要求写作法）；
此时，点P的坐标为 ▲ ，最短周长为 ▲ .
 |
查看习题详情和答案>>
（本题满分10分，第（1）小题4分，第（2）小题6分）
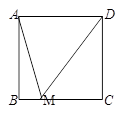
如图，正方形ABCD中， M是边BC上一点，且BM=
.
（1）若
试 用 
表 示 
；
（2）若AB=4
，求sin∠AMD的值.
查看习题详情和答案>>
.
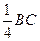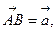
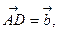试用
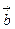表示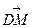
；
