0 447140 447148 447154 447158 447164 447166 447170 447176 447178 447184 447190 447194 447196 447200 447206 447208 447214 447218 447220 447224 447226 447230 447232 447234 447235 447236 447238 447239 447240 447242 447244 447248 447250 447254 447256 447260 447266 447268 447274 447278 447280 447284 447290 447296 447298 447304 447308 447310 447316 447320 447326 447334 447348
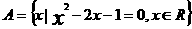 的所有子集个数为( )
的所有子集个数为( )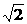 r=2b.
r=2b.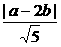 ,∴5d2=(a-2b)2=a2+4b2-4ab≥a2+4b2-2(a2+b2)=2b2-a2=1.当且仅当a=b时“=”号成立,
,∴5d2=(a-2b)2=a2+4b2-4ab≥a2+4b2-2(a2+b2)=2b2-a2=1.当且仅当a=b时“=”号成立, ,由
,由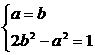 得
得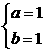 或
或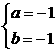 由①得r=
由①得r=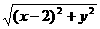 ,即x+2=
,即x+2=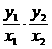 =-1,∴y1y2=-x1x2.
=-1,∴y1y2=-x1x2.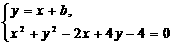 ,得2x2+2(b+1)x+b2+4b-4=0,
,得2x2+2(b+1)x+b2+4b-4=0, +2b-2,y1y2=(x1+b)(x2+b)=x1x2+b(x1+x2)+b2
+2b-2,y1y2=(x1+b)(x2+b)=x1x2+b(x1+x2)+b2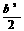 +2b-2-b(b+1)+b2=
+2b-2-b(b+1)+b2= +b-2
+b-2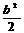 +b-2=-(
+b-2=-(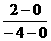 ×k=-1,k=2.
×k=-1,k=2. .
.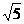 ,∴∠AOB=120°.
,∴∠AOB=120°.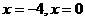 ,满足题意,
,满足题意,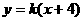 与
与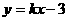 ,
,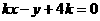 与
与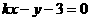 ,由题意:
,由题意: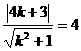 ,解得
,解得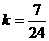 ,
,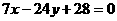 ,
, 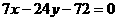
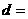
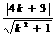 ,∴
,∴ ,
,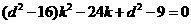 ,
, ∴
∴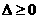 ,即
,即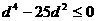 ,
,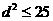 ,∴
,∴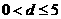 ,∴
,∴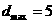 ,当
,当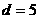 ,
,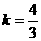 .
.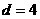 , ∴
, ∴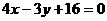 ,
,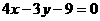 .
.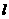 的方程为
的方程为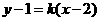 ,
,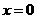 ,得
,得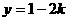 ,故
,故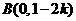 ,
,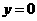 ,得
,得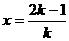 ,故
,故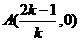 ,
,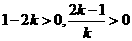 ,所以
,所以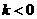 ,
,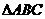 的面积
的面积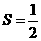
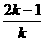
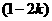
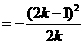
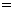
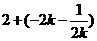 ,
,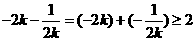 ,从而
,从而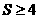 ,
,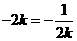 ,即
,即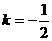 (
(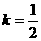 舍去)时,
舍去)时,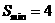 ,
, ,即
,即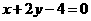 .
.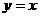 14
14 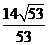 15
15 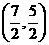 16 (0,5)
16 (0,5)