摘要: 本题主要考查直线.抛物线.不等式等基础知识.求轨迹方程的方法.解析几何的基本思想和综合解题能力.满分12分. 解:(Ⅰ)设P(x1.y1).Q(x2.y2).M(x0.y0).依题意x1≠0.y1>0.y2>0. 由y=x2. ① 得y'=x. ∴过点P的切线的斜率k切= x1. ∴直线l的斜率kl=-=-. ∴直线l的方程为y-x12=- (x-x1). 方法一: 联立①②消去y.得x2+x-x12-2=0. ∵M是PQ的中点 x0==-. ∴ y0=x12-(x0-x1). 消去x1.得y0=x02++1(x0≠0). ∴PQ中点M的轨迹方程为y=x2++1(x≠0). 方法二: 由y1=x12.y2=x22.x0=. 得y1-y2=x12-x22=(x1+x2)(x1-x2)=x0(x1-x2). 则x0==kl=-. ∴x1=-. 将上式代入②并整理.得 y0=x02++1(x0≠0). ∴PQ中点M的轨迹方程为y=x2++1(x≠0). (Ⅱ)设直线l:y=kx+b.依题意k≠0.b≠0.则T(0.b). 分别过P.Q作PP'⊥x轴.QQ'⊥y轴.垂足分别为P'.Q'.则 . y=x2 由 消去x.得y2-2(k2+b)y+b2=0. ③ y=kx+b y1+y2=2(k2+b). 则 y1y2=b2. 方法一: ∴|b|()≥2|b|=2|b|=2. ∵y1.y2可取一切不相等的正数. ∴的取值范围是(2.+). 方法二: ∴=|b|=|b|. 当b>0时.=b==+2>2, 当b<0时.=-b=. 又由方程③有两个相异实根.得△=4(k2+b)2-4b2=4k2(k2+2b)>0. 于是k2+2b>0.即k2>-2b. 所以>=2. ∵当b>0时.可取一切正数. ∴的取值范围是(2.+). 方法三: 由P.Q.T三点共线得kTQ=KTP. 即=. 则x1y2-bx1=x2y1-bx2.即b(x2-x1)=(x2y1-x1y2). 于是b==-x1x2. 2 2 ∴==+=+≥2. ∵可取一切不等于1的正数. ∴的取值范围是(2.+).
网址:http://m.1010jiajiao.com/timu3_id_4465106[举报]
 本题主要考查抛物线的标准方程、简单的几何性质等基础知识,考查运算求解、推理论证的能力.
本题主要考查抛物线的标准方程、简单的几何性质等基础知识,考查运算求解、推理论证的能力.
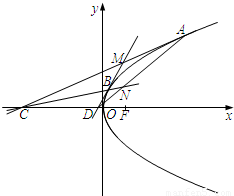
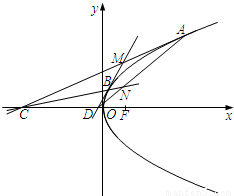
如图,在平面直角坐标系xOy,抛物线的顶点在原点,焦点为F(1,0).过抛物线在x轴上方的不同两点A、B,作抛物线的切线AC、BD,与x轴分别交于C、D两点,且AC与BD交于点M,直线AD与直线BC交于点N.
(1)求抛物线的标准方程;
(2)求证:MN⊥x轴;
(3)若直线MN与x轴的交点恰为F(1,0),求证:直线AB过定点.
查看习题详情和答案>>
本题主要考查抛物线的标准方程、简单的几何性质等基础知识,考查运算求解、推理论证的能力.
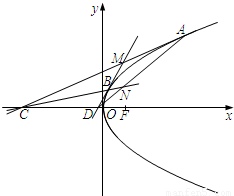
如图,在平面直角坐标系xOy,抛物线的顶点在原点,焦点为F(1,0).过抛物线在x轴上方的不同两点A、B,作抛物线的切线AC、BD,与x轴分别交于C、D两点,且AC与BD交于点M,直线AD与直线BC交于点N.
(1)求抛物线的标准方程;
(2)求证:MN⊥x轴;
(3)若直线MN与x轴的交点恰为F(1,0),求证:直线AB过定点.
 查看习题详情和答案>>
查看习题详情和答案>>
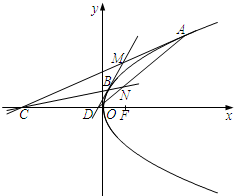
如图,在平面直角坐标系xOy,抛物线的顶点在原点,焦点为F(1,0).过抛物线在x轴上方的不同两点A、B,作抛物线的切线AC、BD,与x轴分别交于C、D两点,且AC与BD交于点M,直线AD与直线BC交于点N.
(1)求抛物线的标准方程;
(2)求证:MN⊥x轴;
(3)若直线MN与x轴的交点恰为F(1,0),求证:直线AB过定点.
 查看习题详情和答案>>
查看习题详情和答案>>
本题主要考查抛物线的标准方程、简单的几何性质等基础知识,考查运算求解、推理论证的能力.
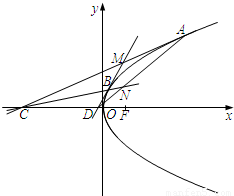
如图,在平面直角坐标系xOy,抛物线的顶点在原点,焦点为F(1,0).过抛物线在x轴上方的不同两点A、B,作抛物线的切线AC、BD,与x轴分别交于C、D两点,且AC与BD交于点M,直线AD与直线BC交于点N.
(1)求抛物线的标准方程;
(2)求证:MN⊥x轴;
(3)若直线MN与x轴的交点恰为F(1,0),求证:直线AB过定点.
 查看习题详情和答案>>
查看习题详情和答案>>
如图,在平面直角坐标系xOy,抛物线的顶点在原点,焦点为F(1,0).过抛物线在x轴上方的不同两点A、B,作抛物线的切线AC、BD,与x轴分别交于C、D两点,且AC与BD交于点M,直线AD与直线BC交于点N.
(1)求抛物线的标准方程;
(2)求证:MN⊥x轴;
(3)若直线MN与x轴的交点恰为F(1,0),求证:直线AB过定点.
 查看习题详情和答案>>
查看习题详情和答案>>