0 446214 446222 446228 446232 446238 446240 446244 446250 446252 446258 446264 446268 446270 446274 446280 446282 446288 446292 446294 446298 446300 446304 446306 446308 446309 446310 446312 446313 446314 446316 446318 446322 446324 446328 446330 446334 446340 446342 446348 446352 446354 446358 446364 446370 446372 446378 446382 446384 446390 446394 446400 446408 447348
 ,
,
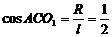 , ………4分所以母线和底面所成的角为
, ………4分所以母线和底面所成的角为 ………6分
………6分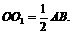 ………8分
………8分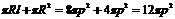 .
………12分
.
………12分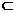 平面ACC1A1,MN
平面ACC1A1,MN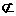 平面ACC1A1,
平面ACC1A1,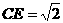 .
.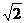 ,求出A1B=2
,求出A1B=2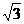 .
.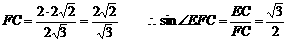
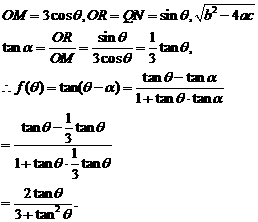
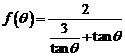 . ………8分
. ………8分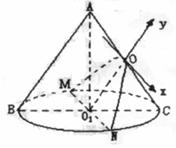 当且仅当
当且仅当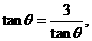 即
即 时,
时,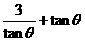 最小值为2
最小值为2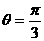 时,
时, 最大,值为
最大,值为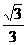 .
.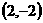 14.
14. 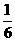 15.
15.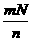 16. 大于
16. 大于 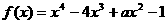 在区间[0,1]单调递增,在区间
在区间[0,1]单调递增,在区间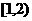 单调递减,
单调递减,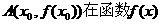 的图象上,求证点A关于直线
的图象上,求证点A关于直线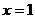 的对称点B也在函数
的对称点B也在函数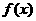 的图象上;
的图象上;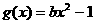 的图象与函数
的图象与函数 与双曲线
与双曲线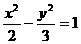 的两个焦点
的两个焦点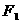 、
、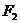 的距离之和为定值,且
的距离之和为定值,且
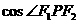 的最小值为
的最小值为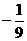 .
.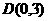 ,
,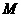 、
、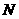 在动点
在动点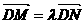 ,求实数
,求实数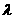 的取值范围.
的取值范围.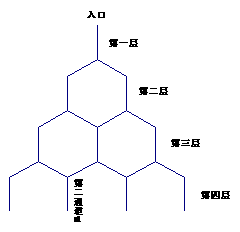 (I)该小弹子落入第4层第2个竖直通道
(I)该小弹子落入第4层第2个竖直通道 层第
层第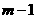 个竖直通道的
个竖直通道的 个竖直通
个竖直通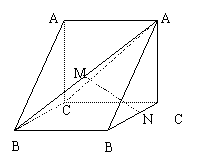 (Ⅰ)求证:MN//平面ACC1A1;
(Ⅰ)求证:MN//平面ACC1A1;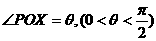 ,Q 是OP上一点,且
,Q 是OP上一点,且 ,过点P,Q向坐标轴作垂线,垂足为M,N,R,记
,过点P,Q向坐标轴作垂线,垂足为M,N,R,记 .
.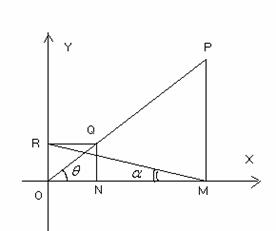 (I) 求函数
(I) 求函数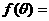

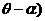 的解析式;
的解析式;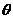 .
.