摘要:解关于x的不等式. 设函数. 的反函数, (Ⅱ)判断在上的单调性并用函数单调性定义加以证明. 某旅游点有50辆自行车供游客租赁使用.管理这些自行车的费用为每日115元.根据经验.若每辆自行车的日租金不超过6元.则自行车可以全部租出,若超过6元.则每超过1元.租不出去的自行车就增加3辆. 为了便于结算.每辆自行车的日租金x(元)只取整数.并且要求出租自行车一日总收入必须高于这一日的管理费用.用y(元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费后的所得). 的解析式及其定义域, (Ⅱ)试问当每辆自行车的日租金定为多少元时.才能使一日的净收入最多? (必要时可参考以下数据:). 如图.AB是圆O的直径.PA垂直于圆O所在的平面.C是圆周上的一点.若A在PC.PB上的射影为D.E. (Ⅰ)求证:AD⊥平面PBC, (Ⅱ)若PA=AB=2.∠BPC=θ.试用tgθ表示△ADE的面积.当tgθ取何值时.△ADE面积最大.最大面积是多少? 第(18)题图 已知抛物线方程为.直线l:x+y=m过抛物线的焦点F且被抛物线截得的弦长为3. (Ⅰ)求p的值, (Ⅱ)是否存在点M.使过点M的斜率不为零的任意直线与抛物线交于P.Q两点.并且以PQ为直径的圆恰过抛物线的顶点?若存在.求出M点的坐标,若不存在.请说明理由. 若和分别表示数列和的前n项的和.对任意正整数n... (Ⅰ)求数列的通项公式, (Ⅱ)在平面直角坐标系内.直线的斜率为.且与曲线有且仅有一个交点.与y轴交于点.记.求, (Ⅲ)若.求证:.
网址:http://m.1010jiajiao.com/timu3_id_4461968[举报]
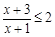 ;
;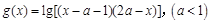 的定义域为B.若
的定义域为B.若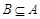 ,求实数a的取值范围.
,求实数a的取值范围.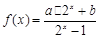 的反函数
的反函数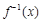 的图象过点
的图象过点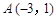 .
.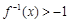 .
. ;
; 的定义域为B.若
的定义域为B.若 ,求实数a的取值范围.
,求实数a的取值范围.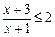 ;
;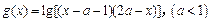 的定义域为B.若
的定义域为B.若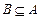 ,求实数a的取值范围.
,求实数a的取值范围.