|
主干知识点 |
知能转化点 |
|
(1)集合、子集、全集、补集的概念 (2)空集和全集的意义 (3)元素与集合的关系;集合与集合的关系 (4)集合的表示法 (5)交集与并集的性质和运算 (6)逻辑联结词“或”、“且”、“否”的含义 (7)四种命题及相互关系 (8)充要条件 |
(1) 集合中的元素的三个特性,是判断一组对象能否组成一个集合的依据 (2)区分有关术语和符号,用符号语言正确表示有关的集合 (3)利用数形结合(包括韦恩图及数轴等)的思想方法,图示各集合间的关系并进行有关集合间的运算 (4)充要条件的判断及用反证法证题 |
|
解题关键点 |
常见障碍点 |
|
(1)理解集合概念,弄清元素与集合、集合与集合的关系 (2)弄清交、并集的区别与联系 (3)“AÍB”Û “A∩B=A”Û“A∪B=B”Û“AÍ A∩B” (4)结合转化思想、数形结合思想等用集合观点来解决“简易逻辑”中的问题 (5)“pÞq”Û{x|p}Í{x|q}”Û“{x|q}Ê{x|p}”Û“p是q的充分条件”Û“q是p的必要条件” |
(1)容易混淆∈与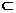 的区别 的区别(2)容易混淆a与{a}的区别 (3)容易混淆空集 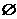 与集合{0}的区别 与集合{0}的区别(4)容易忽视空集为任何集合的子集、非空集合的真子集这一特例 (5)容易遗漏0为自然数的特例 (6)容易混淆充分条件与必要条件的区别 (7)容易混淆命题的否命题与命题的否定的区别 |
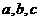 }中的三个不同元素为边长可构成一个三角形,那么这个三角形一定不可能是
( )
}中的三个不同元素为边长可构成一个三角形,那么这个三角形一定不可能是
( )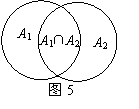 [例11]一次大型会议有2002位代表参加,每位代表至少有1335位合作者.试问这些代表中是否总可以找到四位代表,他们中的每两位都合作过?请证明你的结论.
[例11]一次大型会议有2002位代表参加,每位代表至少有1335位合作者.试问这些代表中是否总可以找到四位代表,他们中的每两位都合作过?请证明你的结论.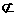 A且C?A的实数a和b是否存在?若存在,求出a,b的所有值;若不存在,请说明理由.
A且C?A的实数a和b是否存在?若存在,求出a,b的所有值;若不存在,请说明理由.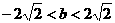 时,方程x2-bx+2=0无解,C=
时,方程x2-bx+2=0无解,C=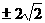 时,方程x2-bx+2=0的解为x=
时,方程x2-bx+2=0的解为x=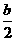 ,C={
,C={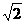 }(当b=
}(当b=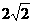 )或C={
)或C={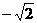 }(当b=
}(当b=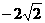 ),此时,不能满足C?A,故b≠
),此时,不能满足C?A,故b≠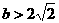 或
或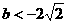 时,方程x2-bx+2=0有两个不等实数根
时,方程x2-bx+2=0有两个不等实数根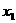 、
、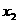 ,于是C={
,于是C={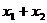 = -p≤0,
= -p≤0,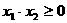 ,解得 p≥2.
,解得 p≥2. .
.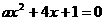 在实数范围内的解的集合.
在实数范围内的解的集合.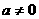 时,⊿=
时,⊿=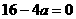 ,a =4,方程有两个相等的实数根
,a =4,方程有两个相等的实数根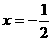 ,P中只有一个元素;当a=0时,方程为一元一次方程,方程只有唯一解
,P中只有一个元素;当a=0时,方程为一元一次方程,方程只有唯一解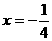 .故当P中只有一个元素时,a=4或0.当a=4时,元素为
.故当P中只有一个元素时,a=4或0.当a=4时,元素为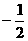 ;当a=0时,元素为
;当a=0时,元素为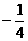 .
. 解得a>4,从而a的取值范围为
解得a>4,从而a的取值范围为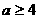 或a=0.
或a=0.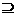 ?UN B.M
?UN B.M ?UN
?UN
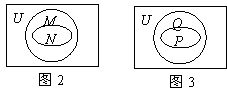 的包含及包含于关系;第(2)小题为1994年上海市高考题,检测由集合的包含关系判断集合的交并关系.两小题均涉及全集、补集、子集及真子集、集合的交并补运算,题中均未给出具体的集合,因而它们不仅全面检测了考生对集合概念理解和掌握程度,也检测了考生的抽象能力,是两道“题小功能大”的好题.对于第(1)小题,作出韦恩图如图2,由图易知?UM
的包含及包含于关系;第(2)小题为1994年上海市高考题,检测由集合的包含关系判断集合的交并关系.两小题均涉及全集、补集、子集及真子集、集合的交并补运算,题中均未给出具体的集合,因而它们不仅全面检测了考生对集合概念理解和掌握程度,也检测了考生的抽象能力,是两道“题小功能大”的好题.对于第(1)小题,作出韦恩图如图2,由图易知?UM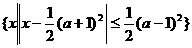 ,B=
,B= .
.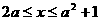 .
.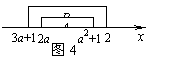 因A Ì B,画出如图4的示意图,由此得
因A Ì B,画出如图4的示意图,由此得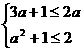
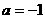 .
.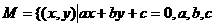 为常数,且a,b不同时为零},
为常数,且a,b不同时为零},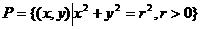 ,则M∩P中的元素个数应为0或1或2.
,则M∩P中的元素个数应为0或1或2.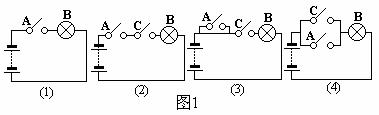 图1 (1)中,开关A闭合是灯泡B亮的 条件;
图1 (1)中,开关A闭合是灯泡B亮的 条件;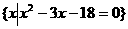 ,B=
,B= .
.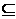 B的等价性将问题进行转化,注意分类讨论思想的运用.
B的等价性将问题进行转化,注意分类讨论思想的运用.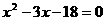 ,得 x= -3或x=6,于是A={-3,6}.
,得 x= -3或x=6,于是A={-3,6}.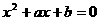 无实数解,于是⊿=
无实数解,于是⊿=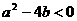 ;
;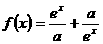 是R上的偶函数。
是R上的偶函数。