0 445764 445772 445778 445782 445788 445790 445794 445800 445802 445808 445814 445818 445820 445824 445830 445832 445838 445842 445844 445848 445850 445854 445856 445858 445859 445860 445862 445863 445864 445866 445868 445872 445874 445878 445880 445884 445890 445892 445898 445902 445904 445908 445914 445920 445922 445928 445932 445934 445940 445944 445950 445958 447348
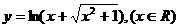 的反函数为( A )
的反函数为( A )
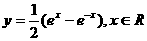 B.
B.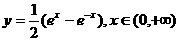
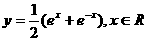 D.
D.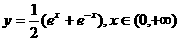
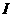 是全集,
是全集,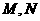 是非空集合,且
是非空集合,且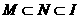 ,则下面结论中不正确的是C
,则下面结论中不正确的是C B.
B.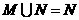 C.
C. D.
D.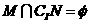
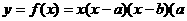 、
、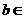 R)。
R)。 ,过两点(0,0)、(
,过两点(0,0)、(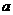 ,0)的中点作与
,0)的中点作与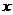 轴垂直的直线,与函数
轴垂直的直线,与函数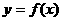 的图象交于点
的图象交于点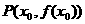 ,求证:函数
,求证:函数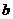 ,0)。
,0)。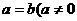 ),且当
),且当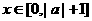 时
时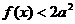 恒成立,求实数
恒成立,求实数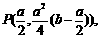 …………1分
…………1分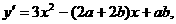 …………2分
…………2分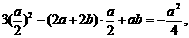 …………3分
…………3分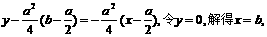
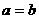 ,所以
,所以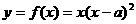 ,
,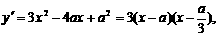 …………5分
…………5分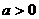 时,函数
时,函数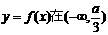 上单调递增,在(
上单调递增,在(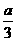 ,
,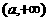 上单调递增. 所以,根据题意有
上单调递增. 所以,根据题意有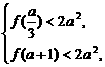 即
即
 ,结合
,结合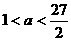 …………8分
…………8分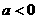 时,函数
时,函数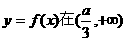 单调递增。
…………9分
单调递增。
…………9分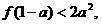 …………10分
…………10分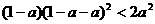 , 整理得
, 整理得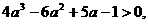 (
( )
)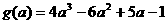 ,
,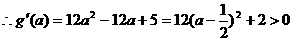
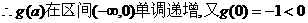 ,所以“
,所以“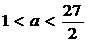 。
…………14分
。
…………14分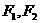 分别是椭圆
分别是椭圆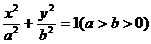 的左右焦点,M为椭圆上一点,
的左右焦点,M为椭圆上一点,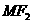 垂直于
垂直于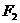 且与OM垂直的直线交椭圆于P,Q.若
且与OM垂直的直线交椭圆于P,Q.若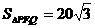 ,求椭圆的方程.
,求椭圆的方程.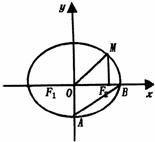
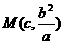
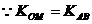
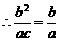
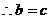 ,
,
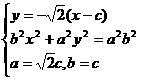
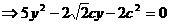

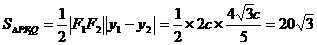
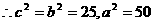
 椭圆的方程为
椭圆的方程为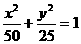
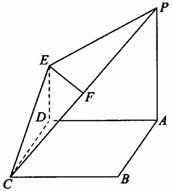 (1)求证:EF//平面ABCD;
(1)求证:EF//平面ABCD;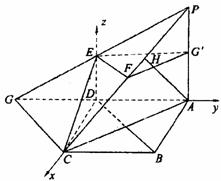 则A(0,2,0),B(2,2,0),C(2,0,0)
则A(0,2,0),B(2,2,0),C(2,0,0) ……2分
……2分
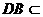 而ABCD 而EF
而ABCD 而EF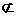 面ABCD
面ABCD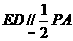 ∴GD=DA=DC ∴△ACG为直角三角形
∴GD=DA=DC ∴△ACG为直角三角形 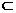 平面ABCD
平面ABCD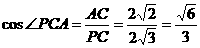 …………8分
…………8分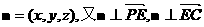
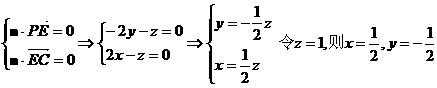
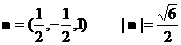 …………6分
…………6分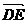 是平面ABCD的法向量,且
是平面ABCD的法向量,且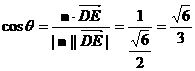 …………8分
…………8分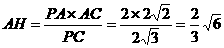 …………12分
…………12分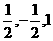 )
)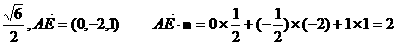
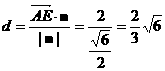 …………
…………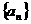 是正数组成的数列,其前n项和为
是正数组成的数列,其前n项和为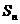 ,且对于所有的正整数n,有
,且对于所有的正整数n,有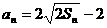 。
。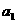 =
=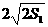 -2 ,
-2 ,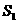 =
= 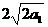 -2 ,解得
-2 ,解得 = 2
= 2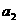 =
=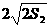 -2 ,
-2 ,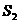 =
= 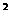 =16,由
=16,由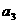 =
=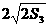 -2 ,
-2 ,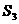 =
= 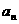 =
=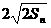 -2(n∈
-2(n∈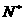 ),
),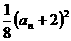 ,
,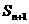 =
=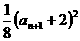
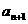 =
=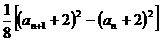
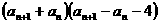 = 0
= 0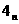 -2,n∈
-2,n∈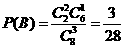
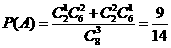
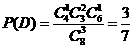
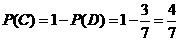 .
.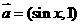 ,
,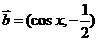 .
.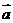 ⊥
⊥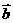 时,求|
时,求|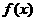 =
=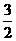 ; (Ⅱ)
; (Ⅱ)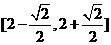 .
.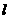 、m是两条不重合的直线,则α∥β的一个充分而不必要条件是
、m是两条不重合的直线,则α∥β的一个充分而不必要条件是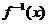 是它的反函数,那么不等式
是它的反函数,那么不等式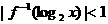 的解集为 .
的解集为 .