15.已知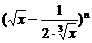 展开式中第4项为常数项,则展开式的各项的系数和为 .
展开式中第4项为常数项,则展开式的各项的系数和为 .
|
 =(-1,2)的直线(点法式)方程为
=(-1,2)的直线(点法式)方程为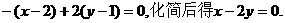 类比以上求法,在空间直角坐标系中,经过点A(2,1,3),且法向量为
类比以上求法,在空间直角坐标系中,经过点A(2,1,3),且法向量为 =(-1,2,1)的平面(点法式)方程为
.(请写出化简后的结果)
=(-1,2,1)的平面(点法式)方程为
.(请写出化简后的结果)
15.已知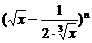 展开式中第4项为常数项,则展开式的各项的系数和为 .
展开式中第4项为常数项,则展开式的各项的系数和为 .
|
 =(-1,2)的直线(点法式)方程为
=(-1,2)的直线(点法式)方程为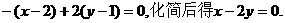 类比以上求法,在空间直角坐标系中,经过点A(2,1,3),且法向量为
类比以上求法,在空间直角坐标系中,经过点A(2,1,3),且法向量为 =(-1,2,1)的平面(点法式)方程为
.(请写出化简后的结果)
=(-1,2,1)的平面(点法式)方程为
.(请写出化简后的结果)