21.(本题12′)设函数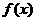 =-
=-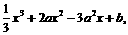 0<
0< <1。
<1。
(1)求函数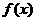 的单调区间、极值。
的单调区间、极值。
(2)若当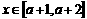 时,恒有
时,恒有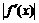 ≤
≤ ,试确定
,试确定 的取值范围。
的取值范围。
[解]:(1)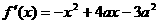 , 令
, 令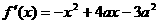 得x=a或x=3a
得x=a或x=3a
由表
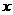 |
(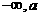 ) ) |
α |
(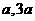 ) ) |
3α |
(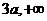 ) ) |
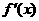 |
- |
0 |
+ |
0 |
- |
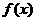 |
递减 |
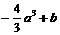 |
递增 |
b |
递减 |
可知:当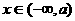 时,函数f (
时,函数f (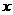 )为减函数,当
)为减函数,当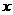
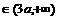 时,函数f(
时,函数f(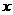 )也为减函数:当
)也为减函数:当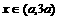 时,函数f(
时,函数f(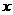 )为增函数。
)为增函数。
(2)由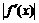 ≤
≤ ,得-
,得- ≤-
≤-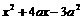 ≤
≤ 。∵0<
。∵0< <1, ∴
<1, ∴ +1>2
+1>2 ,
,
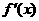 =-
=-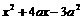 在[
在[ +1,
+1, +2]上为减函数。∴[
+2]上为减函数。∴[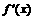 ]max =
]max =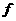 ′(
′( +1)=2
+1)=2 -1,
-1,
[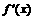 ]min=
]min=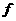 ′(
′( +2)=4
+2)=4 -4.于是,问题转化为求不等式组
-4.于是,问题转化为求不等式组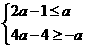 的解。
的解。
解不等式组,得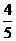 ≤
≤ ≤1。又0<
≤1。又0< <1, ∴所求
<1, ∴所求 的取值范围是
的取值范围是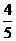 ≤
≤ ≤1。
≤1。
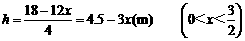 .
.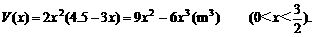
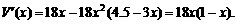
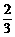 时,V′(x)<0,
时,V′(x)<0, ,因为三位被测试者分别随机抽取一张卡片的事件是相互独立的,因而所求的概率为
,因为三位被测试者分别随机抽取一张卡片的事件是相互独立的,因而所求的概率为
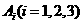 表示所抽取的三张卡片中,恰有
表示所抽取的三张卡片中,恰有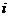 张卡片带有后鼻音“g”的事件,且其相应的概率为
张卡片带有后鼻音“g”的事件,且其相应的概率为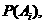 则
则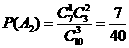 ,
, 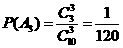
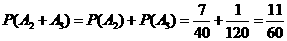
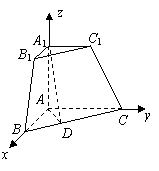
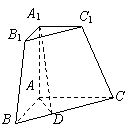 (本题12′)三棱锥被平行于底面
(本题12′)三棱锥被平行于底面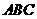 的平面所截得的几何体如图所示,截面为
的平面所截得的几何体如图所示,截面为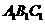 ,
,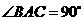 ,
, 平面
平面 ,
, ,
, ,
, ,
,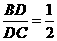 .
.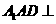 平面
平面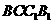 ;
; 的大小.
的大小. ,
,
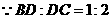 ,
,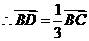 .
. 点坐标为
点坐标为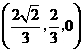 .
.
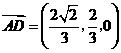 ,
,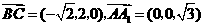 .
.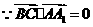 ,
,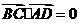 ,
,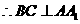 ,
,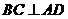 ,又
,又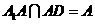 ,
,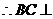 平面
平面 ,又
,又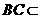 平面
平面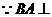 平面
平面 ,取
,取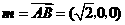 为平面
为平面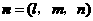 ,则
,则 .
.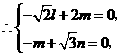
 ,如图,可取
,如图,可取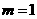 ,则
,则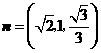 ,
, ,
,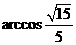 .
. R),若使
R),若使 上为增函数,求a的取值范围.
上为增函数,求a的取值范围. ,由题知:
,由题知: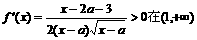 上恒成立
而
上恒成立
而
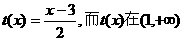 递增且最小值为
递增且最小值为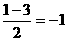 ,
,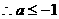
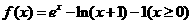 ,则函数f(x)的最小值是 0
,则函数f(x)的最小值是 0 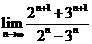 =
-3
=
-3 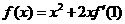 ,
, -2 .
-2 .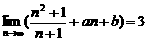 ,则
,则 3 。
3 。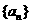 的前
的前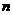 项和
项和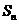 满足
满足 ,那么
,那么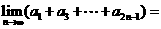 ( C )
( C )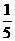 B.
B.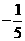 C.
C.