0 445371 445379 445385 445389 445395 445397 445401 445407 445409 445415 445421 445425 445427 445431 445437 445439 445445 445449 445451 445455 445457 445461 445463 445465 445466 445467 445469 445470 445471 445473 445475 445479 445481 445485 445487 445491 445497 445499 445505 445509 445511 445515 445521 445527 445529 445535 445539 445541 445547 445551 445557 445565 447348
 ( )
( )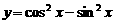 是( )
是( )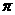 的奇函数 B.周期为
的奇函数 B.周期为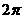 的奇函数
D.周期为
的奇函数
D.周期为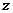 满足
满足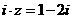 ,则
,则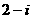 B.
B.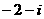 C.
C. D.
D.
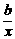 同号.∴|ax+
同号.∴|ax+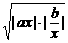 =2
=2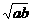 .∴②是真命题.
.∴②是真命题.
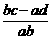 >0,又ab>0
>0,又ab>0 bc-ad>0,即bc>ad,说明由①②
bc-ad>0,即bc>ad,说明由①② ③.同理可证明其他情况.答案:0
③.同理可证明其他情况.答案:0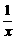 +
+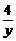 )=5+
)=5+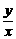 +
+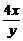 ≥9,又∵x+y=4,∴(
≥9,又∵x+y=4,∴(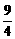 .∴m≤
.∴m≤ ”表示一种运算,即a
”表示一种运算,即a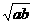 +a+b(a,b为正实数),若1
+a+b(a,b为正实数),若1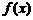 是定义在
是定义在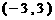 上的奇函数,当
上的奇函数,当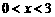 时,
时,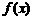 的图象如图所示,则不等式
的图象如图所示,则不等式 的解集
的解集 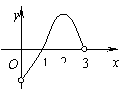 若关于x的方程
若关于x的方程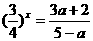 有负实数解,则实数a的取值范围为______;
有负实数解,则实数a的取值范围为______;