0 445394 445402 445408 445412 445418 445420 445424 445430 445432 445438 445444 445448 445450 445454 445460 445462 445468 445472 445474 445478 445480 445484 445486 445488 445489 445490 445492 445493 445494 445496 445498 445502 445504 445508 445510 445514 445520 445522 445528 445532 445534 445538 445544 445550 445552 445558 445562 445564 445570 445574 445580 445588 447348
 的前n项和为Sn,若Sn=2,S30=14,则S40等于( )
的前n项和为Sn,若Sn=2,S30=14,则S40等于( )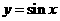 的图象,只需将函数
的图象,只需将函数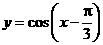 的图象( )
的图象( )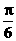 个单位 B.向右平移
个单位 B.向右平移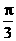 个单位
个单位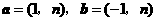 ,若
,若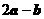 与
与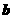 垂直,则
垂直,则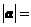 ( )
( )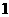 B.
B.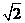 C.
C.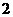 D.4
D.4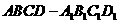 中,
中,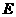 是
是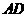 的中点,
的中点,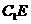 与
与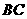 所成的角的余弦值是( )
所成的角的余弦值是( )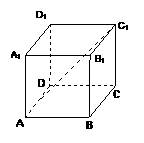 A.
A. B.
B.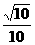
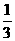 D.
D.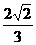
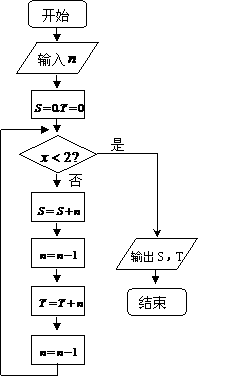 设
设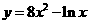 , 则此函数在区间
, 则此函数在区间  和
和 内分别为 ( )
内分别为 ( ) 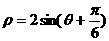 的圆心坐标是 ( )
的圆心坐标是 ( )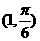 B.
B.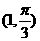 C.
C.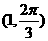 D.
D.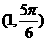

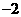 B.
B.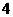
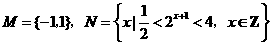 ,则
,则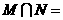 ( )
( )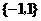 B.
B. C.
C.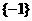 D.
D.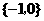
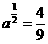 (a>0) ,则
(a>0) ,则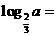 .
.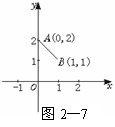 11,
11,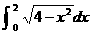 =_____________。
=_____________。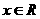 ,
,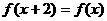 ,②
,② 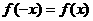 ,
,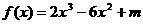 (
( 为常数)在
为常数)在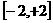 上有最大值
上有最大值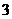 ,那么此函数在
,那么此函数在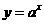 (
(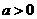 且
且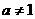 )与函数
)与函数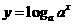 (
(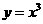 与
与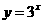 的值域相同;
的值域相同;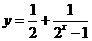 与
与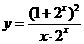 都是奇函数;
都是奇函数;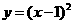 与
与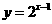 在区间
在区间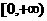 上都是增函数,
上都是增函数,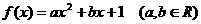 ,
,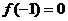 ,且对任意实数
,且对任意实数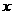 均有
均有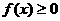 成立,求
成立,求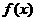 的表达式. (6分)
的表达式. (6分)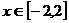 时,
时,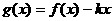 是单调递增函数,求实数
是单调递增函数,求实数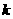 的取值范围。 (6分)
的取值范围。 (6分)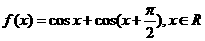
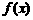 的最小正周期; (3分)
的最小正周期; (3分)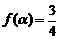 ,求
,求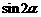 的值. (5分)
的值. (5分)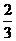 和
和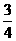 .假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响.
.假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响.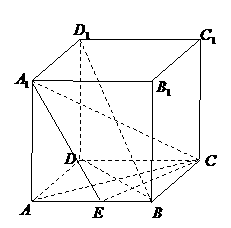 如图,正方体
如图,正方体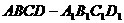 的棱长为2,
的棱长为2,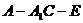 的余弦值;
的余弦值;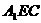 的距离;
的距离;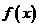 的定义域是
的定义域是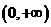 ,对任意正实数
,对任意正实数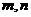 恒有
恒有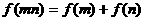 ,且当
,且当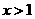 时,
时,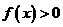 ,
,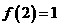
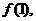
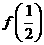 ,
,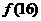 的值; (3分)
的值; (3分)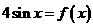 的根的个数.
(6分)
的根的个数.
(6分)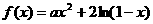 (
(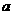 为实数).
为实数).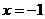 处有极值,求
处有极值,求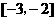 上是增函数,求
上是增函数,求