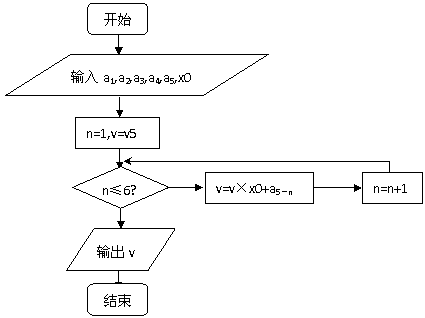
1. 求最大公约数
求最大公约数
(1)辗转相除法
程序框图与程序语句
程序:
INPUT “m,n=”;m,n
DO
r=m MOD n
m=n
n=r
LOOP UNTIL r=0
END
(2)更相减损术
更相减损术程序:
INPUT “请输入两个不相等的正整数”;a,b
i=0
WHILE a MOD 2=0 AND b MOD 2=0
a=a/2
b=b/2
i=i+1
WEND
DO
IF b<a THEN
t=a
a=b
b=t
END IF
c=a-b
a=b
b=c
LOOP UNTIL a=b
PRINT a^i
END
对于两个正整数如何选择合适的方法求他们的最大公约数
|
方法 |
适用范围及特点 |
|
短除法 |
适合两个较小的正整数或两个质因数较少的正整数,简便易操作。 |
|
穷举法 |
适合计算机操作,但一一验证过于繁琐。 |
|
辗转相除法 |
适用于两个较大的正整数,以除法为主,辗转相除法计算次数相对较少,特别当两个数字大小差别较大时计算次数较明显。 |
|
更相减损术 |
适用于两个较大的正整数,更相减损术以减法为主,计算次数上相对于辗转相处法较多。 |
6] -3 0 15
[-3 6] 0 15
[-3 0 6] 15
[-3 0 6 15]
用冒泡排序法排序:
|
6 |
|
6 |
|
6 |
|
6 |
|
6 |
|
6 |
|
6 |
|
15 |
|
15 |
|
15 |
|
-3 |
|
-3 |
|
0 |
|
0 |
|
0 |
|
15 |
|
15 |
|
6 |
|
6 |
|
6 |
|
0 |
|
0 |
|
-3 |
|
15 |
|
15 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
15 |
|
15 |
|
15 |
|
-3 |
|
-3 |
|
-3 |
|
-3 |
|
-3 |
|
-3 |
|
-3 |
题型4:进位值
例7.把十进制数89化为三进制数,并写出程序语句.
解析:具体的计算方法如下:
89=3×29+2
29=3×9+2
9=3×3+0
3=3×1+0
1=3×0+1
所以:89(10)=1011001(3)。
点评:根据三进制数满三进一的原则,可以用3连续去除89及其所的得的商,然后按倒序的先后顺序取出余数组成数据即可。
例8.将8进制数314706(8)化为十进制数,并编写出一个实现算法的程序。
解析:314706(8)=3×85+1×84+4×83+7×82+0×81+6×80=104902。
所以,化为十进制数是104902。
点评:利用把k进制数转化为十进制数的一般方法就可以把8进制数314706(8)化为十进制数,然后根据该算法,利用GET函数,应用循环结构可以设计程序。
7] 1 3 12 8 4 9 10
[7 1] 3 12 8 4 9 10
[7 3 1] 12 8 4 9 10
[12 7 3 1] 8 4 9 10
[12 8 7 3 1] 4 9 10
[12 8 7 4 3 1] 9 10
[12 9 8 7 4 3 1] 10
[12 10 9 8 7 4 3 1]
冒泡排序
|
7 |
|
7 |
|
7 |
|
7 |
|
7 |
|
7 |
|
7 |
|
7 |
|
1 |
1 |
3 |
|
3 |
|
3 |
|
3 |
|
3 |
|
3 |
||
|
3 |
3 |
1 |
|
12 |
|
12 |
|
12 |
|
12 |
|
12 |
||
|
12 |
12 |
12 |
|
1 |
|
8 |
|
8 |
|
8 |
|
8 |
||
|
8 |
8 |
8 |
|
8 |
|
1 |
|
4 |
|
4 |
|
4 |
||
|
4 |
4 |
4 |
|
4 |
|
4 |
|
1 |
|
9 |
|
9 |
||
|
9 |
9 |
9 |
|
9 |
|
9 |
|
9 |
|
1 |
|
10 |
||
|
10 |
10 |
10 |
|
10 |
|
10 |
|
10 |
|
10 |
|
|
第一趟
|
7 |
|
7 |
|
12 |
|
12 |
|
12 |
|
12 |
|
3 |
|
12 |
|
8 |
|
8 |
|
9 |
|
10 |
|
12 |
|
8 |
|
7 |
|
9 |
|
10 |
|
9 |
|
8 |
|
4 |
|
9 |
|
10 |
|
8 |
|
8 |
|
4 |
|
9 |
|
10 |
|
7 |
|
7 |
|
7 |
|
9 |
|
10 |
|
4 |
|
4 |
|
4 |
|
4 |
|
10 |
|
3 |
|
3 |
|
3 |
|
3 |
|
3 |
|
1 |
|
1 |
|
1 |
|
1 |
|
1 |
|
1 |
第2趟 第3趟 第4趟 第5趟 第6趟
点评:直接插入法和冒泡法排序是常见的排序方法,通过该例,我们对比可以发现,直接插入排序比冒泡排序更有效一些,执行的操作步骤更少一些
例6.给出以下四个数:6,-3,0,15,用直接插入法排序将它们按从小到大的顺序排列,用冒泡法将它们按从大到小的顺序排列
分析:不论从大到小的顺序还是按从大到小的顺序,都可按两种方法的步骤进行排序。
解析:
直接插入排序法:

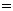


 ≤1,且
≤1,且 在“相关系数检验的临界值表”查出与显著性水平0.05或0.01及自由度n-2(n为观测值组数)相应的相关数临界值r0
在“相关系数检验的临界值表”查出与显著性水平0.05或0.01及自由度n-2(n为观测值组数)相应的相关数临界值r0 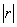 ≤r0.05或r0.01,认为线性关系不显著。
≤r0.05或r0.01,认为线性关系不显著。