0 44404 44412 44418 44422 44428 44430 44434 44440 44442 44448 44454 44458 44460 44464 44470 44472 44478 44482 44484 44488 44490 44494 44496 44498 44499 44500 44502 44503 44504 44506 44508 44512 44514 44518 44520 44524 44530 44532 44538 44542 44544 44548 44554 44560 44562 44568 44572 44574 44580 44584 44590 44598 447348
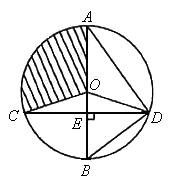 (2006北京海淀)如图,已知⊙O的直径AB垂直于弦CD于E,连结AD、BD、OC、OD,且OD=5。
(2006北京海淀)如图,已知⊙O的直径AB垂直于弦CD于E,连结AD、BD、OC、OD,且OD=5。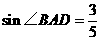 ,求CD的长;
,求CD的长;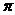 )。
)。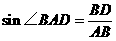
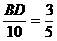 ,所以
,所以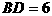
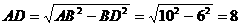
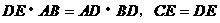
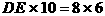
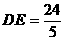
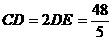
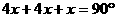

 ∵Rt△AOF中,AF2=m2+n2,
∵Rt△AOF中,AF2=m2+n2,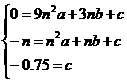
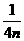 ,b=-
,b=- ,c=-0.75n
,c=-0.75n 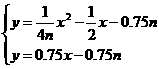
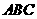 和
和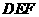 叠放在一起,使三角板
叠放在一起,使三角板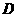 与三角板
与三角板 重合,其中
重合,其中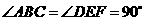 ,
,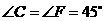 ,
,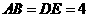 ,把三角板
,把三角板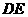 与射线
与射线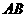 相交于点
相交于点 ,射线
,射线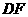 与线段
与线段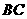 相交于点
相交于点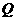 .
.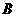 ,即点
,即点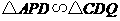 .此时,
.此时, .
. .其中
.其中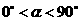 ,问
,问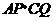 的值是否改变?说明你的理由.
的值是否改变?说明你的理由. (3)在(2)的条件下,设
(3)在(2)的条件下,设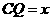 ,两块三角板重叠面积为
,两块三角板重叠面积为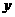 ,求
,求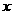 的函数关系式.
的函数关系式.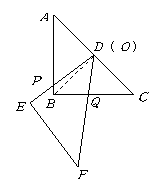 (2)
(2)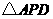 与
与 中,
中,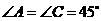
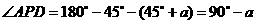
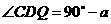
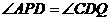

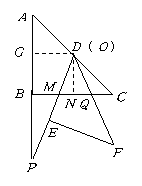 (3)情形1:当
(3)情形1:当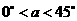 时,
时, ,即
,即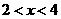 ,此时两三角板重叠部分为四边形
,此时两三角板重叠部分为四边形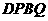 ,过
,过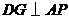 于
于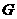 ,
,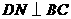 于
于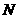 ,
,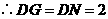
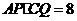 得
得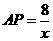
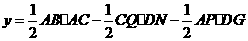
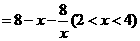
 时,
时, 时,即
时,即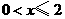 ,此时两三角板重叠部分为
,此时两三角板重叠部分为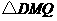 ,
,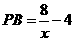 ,易证:
,易证: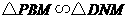 ,
,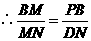 即
即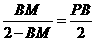 解得
解得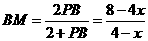
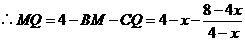
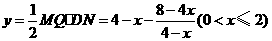
 ,并过
,并过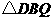 与
与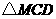 中,
中,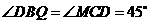
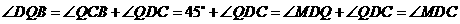


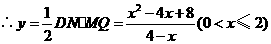
 中,
中,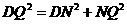
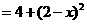

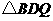 与
与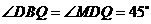



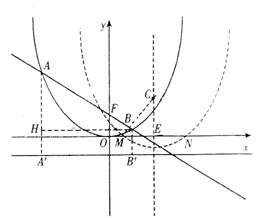
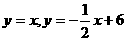 的图象交于点A。动点P从点O开始沿OA方向以每秒1个单位的速度运动,作PQ∥x轴交直线BC于点Q,以PQ为一边向下作正方形PQMN,设它与△OAB重叠部分的面积为S。
的图象交于点A。动点P从点O开始沿OA方向以每秒1个单位的速度运动,作PQ∥x轴交直线BC于点Q,以PQ为一边向下作正方形PQMN,设它与△OAB重叠部分的面积为S。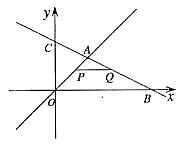 (1)求点A的坐标。
(1)求点A的坐标。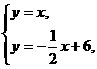 可得
可得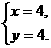
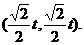
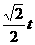 ,并且点Q在
,并且点Q在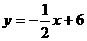 上。
上。 ,
,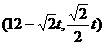 。
。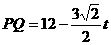 。
。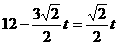 时,
时,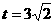 。
。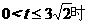 ,
,
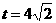 ,
,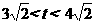 时,
时,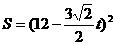
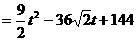 。
。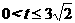 中,
中,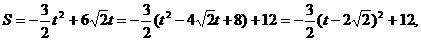
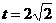 时,S的最大值为12。
时,S的最大值为12。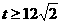 。
。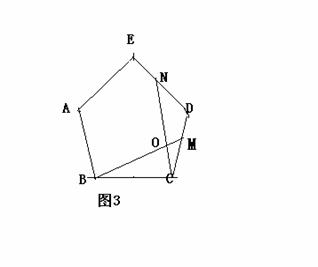
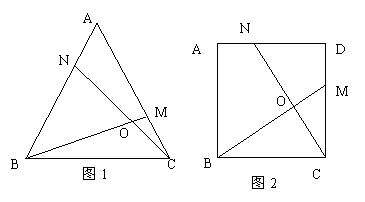
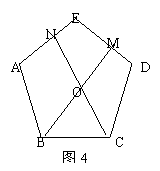
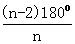 时结论BM=CN成立.
时结论BM=CN成立. 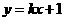 的图象与二次函数的图象交于
的图象与二次函数的图象交于 两点(
两点( 在
在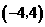 .平行于
.平行于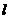 过
过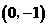 点.
点.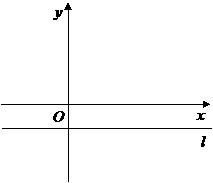 (3)把二次函数的图象向右平移
(3)把二次函数的图象向右平移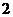 个单位,再向下平移
个单位,再向下平移 个单位
个单位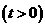 ,二次函数的图象与
,二次函数的图象与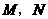 两点,一次函数图象交
两点,一次函数图象交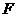 点.当
点.当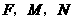 三点的圆的面积最小?最小面积是多少?
三点的圆的面积最小?最小面积是多少?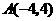 代入
代入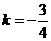 ,
, 一次函数的解析式为
一次函数的解析式为 ;
;  二次函数图象的顶点在原点,对称轴为
二次函数图象的顶点在原点,对称轴为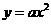 ,
, ,
,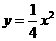 .
. 
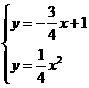
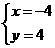 或
或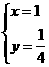 ,
, ,
, 点分别作直线
点分别作直线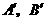 ,
,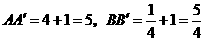 ,
,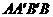 的中位线长为
的中位线长为 ,
,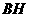 垂直于直线
垂直于直线 于点
于点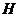 ,则
,则 ,
,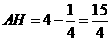 ,
,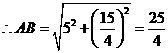 ,
,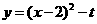 ,
, ,得
,得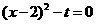 ,
,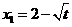 ,
,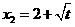 ,
,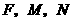 三点的圆的圆心一定在直线
三点的圆的圆心一定在直线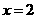 上,点
上,点 ,
,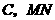 中点为
中点为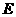 ,连
,连 ,则
,则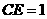 ,
, 中,
中,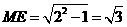 ,
,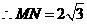 ,而
,而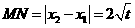 ,
,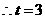 ,
,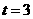 时,过
时,过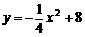 ,BC所在抛物线的解析式为
,BC所在抛物线的解析式为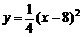 ,且已知
,且已知 .
.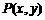 是山坡线AB上任意一点,用y表示x,并求点B的坐标;
是山坡线AB上任意一点,用y表示x,并求点B的坐标; (米).假设索道DE可近似地看成一
(米).假设索道DE可近似地看成一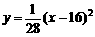 .试求索道的最大悬空高度.
.试求索道的最大悬空高度.
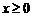 ,
,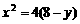 ,
,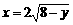
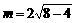 =4,∴
=4,∴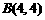
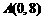
 ,得
,得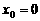 ;令
;令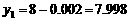 ,得
,得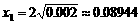
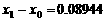 (百米)
(百米)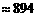 (厘米)
(厘米)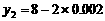 、
、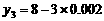 ,可得
,可得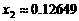 、
、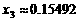
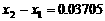 (百米)
(百米)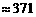 (厘米)
(厘米) (百米)
(百米)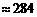 (厘米)
(厘米)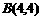 ,又取
,又取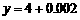 ,则
,则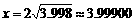

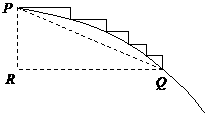 ②另解:连接任意一段台阶的两端点P、Q,如图
②另解:连接任意一段台阶的两端点P、Q,如图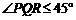

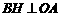 于H
于H ,又第一级台阶的长大于它的高
,又第一级台阶的长大于它的高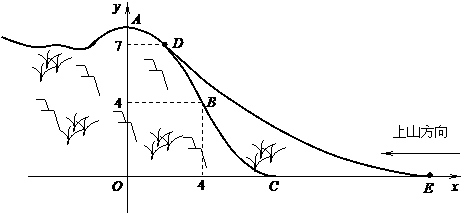 (3)
(3)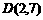 、
、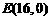 、
、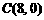
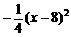
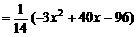

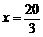 时,
时,
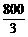 米.
米.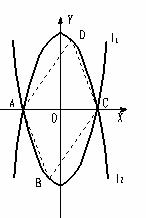 (3)探索:当点B分别位于l1在x轴上、下两部分的图像上时,平行四边形ABCD的面积是否存在最大值和最小值?若存在,判断它是何种特殊平行四边形,并求出它的面积;若不存在,请说明理由。
(3)探索:当点B分别位于l1在x轴上、下两部分的图像上时,平行四边形ABCD的面积是否存在最大值和最小值?若存在,判断它是何种特殊平行四边形,并求出它的面积;若不存在,请说明理由。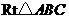 中,
中,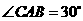 ,
,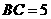 .过点
.过点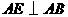 ,且
,且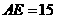 ,连接
,连接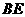 交
交 于点
于点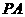 的长;
的长;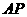 为半径作⊙A,试判断
为半径作⊙A,试判断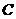 作
作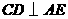 ,垂足为
,垂足为 为半径作⊙A;以点
为半径作⊙A;以点 为半径作⊙C.若
为半径作⊙C.若
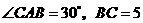 ,
,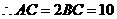 .
. 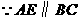 ,
,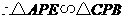 .
.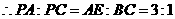 .
. ,
,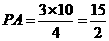 .
.  中,
中,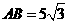 ,
,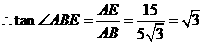 ,
,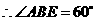 .
.  ,
,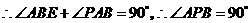 ,
,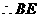 与⊙A相切.
与⊙A相切. 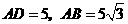 ,所以
,所以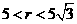 .
. 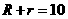 ,所以
,所以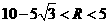 ;
;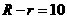 ,所以
,所以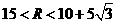 .
. 如图,平面直角坐标系中,直线AB与
如图,平面直角坐标系中,直线AB与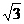 )两点, ,点C为线段AB上的一动点,过点C作CD⊥
)两点, ,点C为线段AB上的一动点,过点C作CD⊥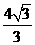 ,求点C的坐标;
,求点C的坐标;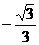 x+
x+ =
=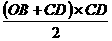 =
=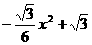 .
.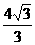 ,解得
,解得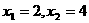 (舍去)
(舍去) )
)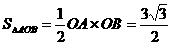 ,
,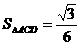 .
.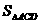 =
=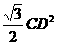 =
=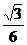 .可得CD=
.可得CD= ∴ AD=1,OD=2.∴C(2,
∴ AD=1,OD=2.∴C(2,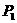 (3,
(3,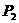 (1,
(1,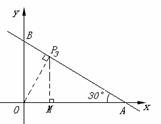 过点P作PM⊥OA于点M.
过点P作PM⊥OA于点M.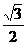 ,OP=
,OP=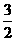 .
.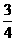 ;PM=
;PM=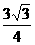 .∴
.∴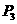 (
(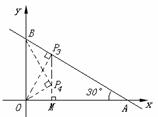 方法二:设P(x ,
方法二:设P(x ,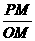 =
=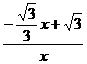 ,tan∠ABOC=
,tan∠ABOC=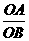 =
=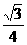 .
.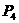 (
(