摘要：如图.点O是坐标原点.点A(n.0)是x轴上一动点(n＜0＝以AO为一边作矩形AOBC.点C在第二象限.且OB＝2OA．矩形AOBC绕点A逆时针旋转90o得矩形AGDE．过点A的直线y＝kx+m 交y轴于点F.FB＝FA．抛物线y=ax2+bx+c过点E.F.G且和直线AF交于点H.过点H作HM⊥x轴.垂足为点M．(1)求k的值, (2)点A位置改变时.△AMH的面积和矩形AOBC 的面积的比值是否改变?说明你的理由． [解] (1)根据题意得到:E 当x＝0时.y＝kx+m＝m.∴点F坐标为(0.m) ∵Rt△AOF中.AF2＝m2+n2. ∵FB＝AF. ∴m2+n2＝2. 化简得:m＝-0.75n. 对于y＝kx+m.当x＝n时.y＝0. ∴0＝kn-0.75n. ∴k＝0.75 (2)∵抛物线y=ax2+bx+c过点E.F.G. ∴ 解得:a＝.b＝-.c＝-0.75n ∴抛物线为y=x2-x-0.75n 解方程组: 得:x1＝5n.y1＝3n,x2＝0.y2＝-0.75n ∴H坐标是:.HM＝-3n.AM＝n-5n＝-4n. ∴△AMH的面积＝0.5×HM×AM＝6n2, 而矩形AOBC 的面积＝2n2.∴△AMH的面积∶矩形AOBC 的面积＝3:1.不随着点A的位置的改变而改变．
网址：http://m.1010jiajiao.com/timu3_id_445019[举报]
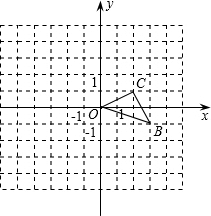如图已知O是坐标原点，B、C两点的坐标分别为（3，-1）、（2，1）（1）画出以O点为旋转中心逆时针旋转90度得到的△B′OC′，并写出B、C两点的对应点B′、C′的坐标；
（2）求点C旋转到点C′所经过的路线长（结果保留π）．
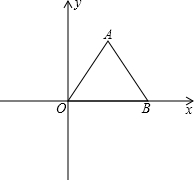如图，△AOB是等边三角形，点O是坐标原点，点B的坐标为（2，0）（1）求点A的坐标；
（2）将△ABO绕点A逆时针旋转180°后，求点B的对应点B′的坐标；
（3）将△ABO绕点A逆时针旋转90°后，求点B的对应点B″的坐标． 查看习题详情和答案>>
已知，在直角坐标系中，△ABO的位置如图1，点O是坐标原点，点A的坐标为（-3，4），AB=AO，AB∥x轴交于y轴于点H．
（1）填空：点B的坐标（
（2）把△ABO沿直线OB翻折得到△CBO，连接AC交于y轴于点M，请在图2 中画出图形，并判断此时四边形AOCB的形状，说明理由．
（3）连接BM，动点P从点A出发，沿折线ABC方向向终点C匀速运动，点P的运动时间为t秒，点P的速度为每秒2个单位，设△PMB的面积为S（S≠0），求当t为何值时，S有最大值，并求出S的最大值．
（4）在（3）条件下，点P在运动过程中，当∠MPB+∠BCO=90°时，求直线OP与直线AC所夹锐角的正切值．
查看习题详情和答案>>
（1）填空：点B的坐标（
2
2
，4
4
），△ABO的面积是10
10
．（2）把△ABO沿直线OB翻折得到△CBO，连接AC交于y轴于点M，请在图2 中画出图形，并判断此时四边形AOCB的形状，说明理由．
（3）连接BM，动点P从点A出发，沿折线ABC方向向终点C匀速运动，点P的运动时间为t秒，点P的速度为每秒2个单位，设△PMB的面积为S（S≠0），求当t为何值时，S有最大值，并求出S的最大值．
（4）在（3）条件下，点P在运动过程中，当∠MPB+∠BCO=90°时，求直线OP与直线AC所夹锐角的正切值．
标为（-2，0）．
如图，等腰△AOC的底边OC在x轴的正半轴，点O是坐标原点，点A在第一象限，若AO=5，OC=6，则顶点A的坐标是