摘要:22.在圆内接四边形ABCD中.CD为∠BCA外角的平分线.F为弧AD上一点.BC=AF.延长DF与BA的延长线交于E. ⑴求证△ABD为等腰三角形. ⑵求证AC•AF=DF•FE [解题思路](1)利用同角的补角相等.同弧所对的圆周角相等.等量代换, (2)证等积式就要找三角形相似.发现AC.AF.FE所在的三角形.且利用等弧对等弦.同圆中等弦对等弧.发现DF可以被DC替换.进而求解. [答案]⑴由圆的性质知∠MCD=∠DAB.∠DCA=∠DBA.而∠MCD=∠DCA.所以∠DBA=∠DAB.故△ABD为等腰三角形. ⑵∵∠DBA=∠DAB ∴弧AD=弧BD 又∵BC=AF ∴弧BC=弧AF.∠CDB=∠FDA ∴弧CD=弧DF ∴CD=DF 再由“圆的内接四边形外角等于它的内对角 知 ∠AFE=∠DBA=∠DCA①.∠FAE=∠BDE ∴∠CDA=∠CDB+∠BDA=∠FDA+∠BDA=∠BDE=∠FAE② 由①②得△DCA∽△FAE ∴AC:FE=CD:AF ∴AC•AF= CD •FE 而CD=DF. ∴AC•AF=DF•FE [点评]解决此题关键要用到与圆相关的性质.定理以及三角形相似的判定.等角对等边. 有一定的几何知识的综合性.考查学生审图.分析图中边角关系的解题技能. 难度中等
网址:http://m.1010jiajiao.com/timu3_id_435872[举报]
如图,在圆内接四边形ABCD中,CD为∠BCA的外角的平分线,F为
上一点,BC=AF,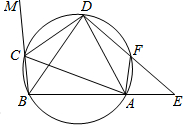 延长DF与BA的延长线交于E.
延长DF与BA的延长线交于E.
(1)求证:△ABD为等腰三角形.
(2)求证:AC•AF=DF•FE. 查看习题详情和答案>>
 | AD |
 延长DF与BA的延长线交于E.
延长DF与BA的延长线交于E.(1)求证:△ABD为等腰三角形.
(2)求证:AC•AF=DF•FE. 查看习题详情和答案>>
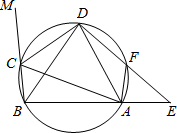 如图在圆内接四边形ABCD中,CD为∠BCA外角的平分线,F为
如图在圆内接四边形ABCD中,CD为∠BCA外角的平分线,F为 如图,在圆内接四边形ABCD中,AB=AD,∠BAD=60°,AC=a,则四边形ABCD的面积为
如图,在圆内接四边形ABCD中,AB=AD,∠BAD=60°,AC=a,则四边形ABCD的面积为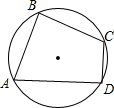 如图,在圆内接四边形ABCD中,∠A=60°,∠B=90°,AB=2,CD=1,则BC=
如图,在圆内接四边形ABCD中,∠A=60°,∠B=90°,AB=2,CD=1,则BC= 如图,在圆内接四边形ABCD中,若∠C=80°,则∠A等于( )
如图,在圆内接四边形ABCD中,若∠C=80°,则∠A等于( )